Part of a series on
Evolutionary biology
Darwin's finches by John Gould
Index Introduction Main Outline Glossary Evidence History
Processes and outcomes Population genetics Variation Diversity Mutation Natural selection Adaptation Polymorphism Genetic drift Gene flow Speciation Adaptive radiation Co-operation Coevolution Coextinction Contingency Divergence Convergence Parallel evolution Extinction
Natural history Origin of life Common descent History of life Timeline of evolution Human evolution Phylogeny Biodiversity Biogeography Classification Evolutionary taxonomy Cladistics Transitional fossil Extinction event
History of evolutionary theory Overview Renaissance Before Darwin Darwin Origin of Species Before synthesis Modern synthesis Molecular evolution Evo-devo Current research History of speciation History of paleontology (timeline)
Fields and applications Applications of evolution Biosocial criminology Ecological genetics Evolutionary aesthetics Evolutionary anthropology Evolutionary computation Evolutionary ecology Evolutionary economics Evolutionary epistemology Evolutionary ethics Evolutionary game theory Evolutionary linguistics Evolutionary medicine Evolutionary neuroscience Evolutionary physiology Evolutionary psychology Experimental evolution Phylogenetics Paleontology Selective breeding Speciation experiments Sociobiology Island biogeography Systematics Universal Darwinism
Social implications Evolution as fact and theory Social effects Creation–evolution controversy Theistic evolution Objections to evolution Level of support Nature-nurture controversy
Evolutionary biology portal  Category
v t e

Genetic drift, also known as random genetic drift, allelic drift or the Wright effect,^[1] is the change in the frequency of an existing gene variant (allele) in a population due to random chance.^[2]

Genetic drift may cause gene variants to disappear completely and thereby reduce genetic variation.^[3] It can also cause initially rare alleles to become much more frequent and even fixed.

When few copies of an allele exist, the effect of genetic drift is more notable, and when many copies exist, the effect is less notable (due to the law of large numbers). In the middle of the 20th century, vigorous debates occurred over the relative importance of natural selection versus neutral processes, including genetic drift. Ronald Fisher, who explained natural selection using Mendelian genetics,^[4] held the view that genetic drift plays at most a minor role in evolution, and this remained the dominant view for several decades. In 1968, population geneticist Motoo Kimura rekindled the debate with his neutral theory of molecular evolution, which claims that most instances where a genetic change spreads across a population (although not necessarily changes in phenotypes) are caused by genetic drift acting on neutral mutations.^[5][6] In the 1990s, constructive neutral evolution was proposed which seeks to explain how complex systems emerge through neutral transitions.^[7][8]

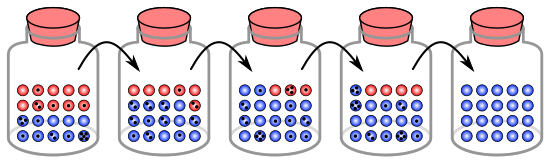
Analogy with marbles in a jar

The process of genetic drift can be illustrated using 20 marbles in a jar to represent 20 organisms in a population.^[9] Consider this jar of marbles as the starting population. Half of the marbles in the jar are red and half are blue, with each colour corresponding to a different allele of one gene in the population. In each new generation, the organisms reproduce at random. To represent this reproduction, randomly select a marble from the original jar and deposit a new marble with the same colour into a new jar. This is the "offspring" of the original marble, meaning that the original marble remains in its jar. Repeat this process until 20 new marbles are in the second jar. The second jar will now contain 20 "offspring", or marbles of various colours. Unless the second jar contains exactly 10 red marbles and 10 blue marbles, a random shift has occurred in the allele frequencies.

If this process is repeated a number of times, the numbers of red and blue marbles picked each generation fluctuates. Sometimes, a jar has more red marbles than its "parent" jar and sometimes more blue. This fluctuation is analogous to genetic drift – a change in the population's allele frequency resulting from a random variation in the distribution of alleles from one generation to the next.

In any one generation, no marbles of a particular colour could be chosen, meaning they have no offspring. In this example, if no red marbles are selected, the jar representing the new generation contains only blue offspring. If this happens, the red allele has been lost permanently in the population, while the remaining blue allele has become fixed: all future generations are entirely blue. In small populations, fixation can occur in just a few generations.

Probability and allele frequency

The mechanisms of genetic drift can be illustrated with a simplified example. Consider a very large colony of bacteria isolated in a drop of solution. The bacteria are genetically identical except for a single gene with two alleles labeled A and B, which are neutral alleles, meaning that they do not affect the bacteria's ability to survive and reproduce; all bacteria in this colony are equally likely to survive and reproduce. Suppose that half the bacteria have allele A and the other half have allele B. Thus, A and B each has an allele frequency of 1/2.

The drop of solution then shrinks until it has only enough food to sustain four bacteria. All other bacteria die without reproducing. Among the four that survive, 16 possible combinations for the A and B alleles exist:
(A-A-A-A), (B-A-A-A), (A-B-A-A), (B-B-A-A),
(A-A-B-A), (B-A-B-A), (A-B-B-A), (B-B-B-A),
(A-A-A-B), (B-A-A-B), (A-B-A-B), (B-B-A-B),
(A-A-B-B), (B-A-B-B), (A-B-B-B), (B-B-B-B).

Since all bacteria in the original solution are equally likely to survive when the solution shrinks, the four survivors are a random sample from the original colony. The probability that each of the four survivors has a given allele is 1/2, and so the probability that any particular allele combination occurs when the solution shrinks is

${\displaystyle {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}={\frac {1}{16}}.}$

(The original population size is so large that the sampling effectively happens with replacement). In other words, each of the 16 possible allele combinations is equally likely to occur, with probability 1/16.

Counting the combinations with the same number of A and B gives the following table:

As shown in the table, the total number of combinations that have the same number of A alleles as of B alleles is six, and the probability of this combination is 6/16. The total number of other combinations is ten, so the probability of unequal number of A and B alleles is 10/16. Thus, although the original colony began with an equal number of A and B alleles, quite possibly, the number of alleles in the remaining population of four members will not be equal. The situation of equal numbers is actually less likely than unequal numbers. In the latter case, genetic drift has occurred because the population's allele frequencies have changed due to random sampling. In this example, the population contracted to just four random survivors, a phenomenon known as a population bottleneck.

The probabilities for the number of copies of allele A (or B) that survive (given in the last column of the above table) can be calculated directly from the binomial distribution, where the "success" probability (probability of a given allele being present) is 1/2 (i.e., the probability that there are k copies of A (or B) alleles in the combination) is given by:

${\displaystyle {n \choose k}\left({\frac {1}{2}}\right)^{k}\left(1-{\frac {1}{2}}\right)^{n-k}={n \choose k}\left({\frac {1}{2}}\right)^{n}\!}$

where n=4 is the number of surviving bacteria.

Mathematical models

Mathematical models of genetic drift can be designed using either branching processes or a diffusion equation describing changes in allele frequency in an idealised population.^[10]

Wright–Fisher model

Consider a gene with two alleles, A or B. In diploidy, populations consisting of N individuals have 2N copies of each gene. An individual can have two copies of the same allele or two different alleles. The frequency of one allele is assigned p and the other q. The Wright–Fisher model (named after Sewall Wright and Ronald Fisher) assumes that generations do not overlap (for example, annual plants have exactly one generation per year) and that each copy of the gene found in the new generation is drawn independently at random from all copies of the gene in the old generation. The formula to calculate the probability of obtaining k copies of an allele that had frequency p in the last generation is then^[11][12]

${\displaystyle {\frac {(2N)!}{k!(2N-k)!}}p^{k}q^{2N-k}}$

where the symbol "!" signifies the factorial function. This expression can also be formulated using the binomial coefficient,

${\displaystyle {2N \choose k}p^{k}q^{2N-k}}$

Moran model

The Moran model assumes overlapping generations. At each time step, one individual is chosen to reproduce and one individual is chosen to die. So in each timestep, the number of copies of a given allele can go up by one, go down by one, or can stay the same. This means that the transition matrix is tridiagonal, which means that mathematical solutions are easier for the Moran model than for the Wright–Fisher model. On the other hand, computer simulations are usually easier to perform using the Wright–Fisher model, because fewer time steps need to be calculated. In the Moran model, it takes N timesteps to get through one generation, where N is the effective population size. In the Wright–Fisher model, it takes just one.^[13]

In practice, the Moran and Wright–Fisher models give qualitatively similar results, but genetic drift runs twice as fast in the Moran model.

Other models of drift

If the variance in the number of offspring is much greater than that given by the binomial distribution assumed by the Wright–Fisher model, then given the same overall speed of genetic drift (the variance effective population size), genetic drift is a less powerful force compared to selection.^[14] Even for the same variance, if higher moments of the offspring number distribution exceed those of the binomial distribution then again the force of genetic drift is substantially weakened.^[15]

Random effects other than sampling error

Random changes in allele frequencies can also be caused by effects other than sampling error, for example random changes in selection pressure.^[16]

One important alternative source of stochasticity, perhaps more important than genetic drift, is genetic draft.^[17] Genetic draft is the effect on a locus by selection on linked loci. The mathematical properties of genetic draft are different from those of genetic drift.^[18] The direction of the random change in allele frequency is autocorrelated across generations.^[2]

Drift and fixation

The Hardy–Weinberg principle states that within sufficiently large populations, the allele frequencies remain constant from one generation to the next unless the equilibrium is disturbed by migration, genetic mutations, or selection.^[19]

However, in finite populations, no new alleles are gained from the random sampling of alleles passed to the next generation, but the sampling can cause an existing allele to disappear. Because random sampling can remove, but not replace, an allele, and because random declines or increases in allele frequency influence expected allele distributions for the next generation, genetic drift drives a population towards genetic uniformity over time. When an allele reaches a frequency of 1 (100%) it is said to be "fixed" in the population and when an allele reaches a frequency of 0 (0%) it is lost. Smaller populations achieve fixation faster, whereas in the limit of an infinite population, fixation is not achieved. Once an allele becomes fixed, genetic drift comes to a halt, and the allele frequency cannot change unless a new allele is introduced in the population via mutation or gene flow. Thus even while genetic drift is a random, directionless process, it acts to eliminate genetic variation over time.^[20]

Rate of allele frequency change due to drift

Assuming genetic drift is the only evolutionary force acting on an allele, after t generations in many replicated populations, starting with allele frequencies of p and q, the variance in allele frequency across those populations is

${\displaystyle V_{t}\approx pq\left(1-\exp \left(-{\frac {t}{2N_{e}}}\right)\right)}$^[21]

Time to fixation or loss

Assuming genetic drift is the only evolutionary force acting on an allele, at any given time the probability that an allele will eventually become fixed in the population is simply its frequency in the population at that time.^[22] For example, if the frequency p for allele A is 75% and the frequency q for allele B is 25%, then given unlimited time the probability A will ultimately become fixed in the population is 75% and the probability that B will become fixed is 25%.

The expected number of generations for fixation to occur is proportional to the population size, such that fixation is predicted to occur much more rapidly in smaller populations.^[23] Normally the effective population size, which is smaller than the total population, is used to determine these probabilities. The effective population (N_e) takes into account factors such as the level of inbreeding, the stage of the lifecycle in which the population is the smallest, and the fact that some neutral genes are genetically linked to others that are under selection.^[14] The effective population size may not be the same for every gene in the same population.^[24]

One forward-looking formula used for approximating the expected time before a neutral allele becomes fixed through genetic drift, according to the Wright–Fisher model, is

${\displaystyle {\bar {T}}_{\text{fixed}}={\frac {-4N_{e}(1-p)\ln(1-p)}{p}}}$

where T is the number of generations, N_e is the effective population size, and p is the initial frequency for the given allele. The result is the number of generations expected to pass before fixation occurs for a given allele in a population with given size (N_e) and allele frequency (p).^[25]

The expected time for the neutral allele to be lost through genetic drift can be calculated as^[11]

${\displaystyle {\bar {T}}_{\text{lost}}={\frac {-4N_{e}p}{1-p}}\ln p.}$

When a mutation appears only once in a population large enough for the initial frequency to be negligible, the formulas can be simplified to^[26]

${\displaystyle {\stackrel{¯<!--\; ¯\; -->}{T}}_{\text{fixed}}=4N_e}$Zdroj:https://en.wikipedia.org?pojem=Genetic_drift
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---