In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon,^[1] who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes (integrating over lines is known as the X-ray transform). It was later generalized to higher-dimensional Euclidean spaces and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.

Explanation

If a function${\displaystyle f}$ represents an unknown density, then the Radon transform represents the projection data obtained as the output of a tomographic scan. Hence the inverse of the Radon transform can be used to reconstruct the original density from the projection data, and thus it forms the mathematical underpinning for tomographic reconstruction, also known as iterative reconstruction.

The Radon transform data is often called a sinogram because the Radon transform of an off-center point source is a sinusoid. Consequently, the Radon transform of a number of small objects appears graphically as a number of blurred sine waves with different amplitudes and phases.

The Radon transform is useful in computed axial tomography (CAT scan), barcode scanners, electron microscopy of macromolecular assemblies like viruses and protein complexes, reflection seismology and in the solution of hyperbolic partial differential equations.

Definition

Let ${\displaystyle f({\textbf {x}})=f(x,y)}$ be a function that satisfies the three regularity conditions:^[3]

1. ${\displaystyle f({\textbf {x}})}$ is continuous;
2. the double integral ${\displaystyle \iint {\dfrac {\vert f({\textbf {x}})\vert }{\sqrt {x^{2}+y^{2}}}}\,dx\,dy}$, extending over the whole plane, converges;
3. for any arbitrary point ${\displaystyle (x,y)}$ on the plane it holds that ${\displaystyle \lim _{r\to \infty }\int _{0}^{2\pi }f(x+r\cos \varphi ,y+r\sin \varphi )\,d\varphi =0.}$

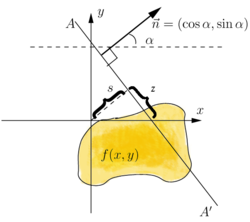
The Radon transform, ${\displaystyle Rf}$, is a function defined on the space of straight lines ${\displaystyle L\subset \mathbb {R} ^{2}}$ by the line integral along each such line as: $${\displaystyle Rf(L)=\int _{L}f(\mathbf {x} )\vert d\mathbf {x} \vert .}$$Concretely, the parametrization of any straight line ${\displaystyle L}$ with respect to arc length ${\displaystyle z}$ can always be written:$${\displaystyle (x(z),y(z))={\Big (}(z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ){\Big )}\,}$$where ${\displaystyle s}$ is the distance of ${\displaystyle L}$ from the origin and ${\displaystyle \alpha }$ is the angle the normal vector to ${\displaystyle L}$ makes with the ${\displaystyle X}$-axis. It follows that the quantities ${\displaystyle (\alpha ,s)}$ can be considered as coordinates on the space of all lines in ${\displaystyle \mathbb {R} ^{2}}$, and the Radon transform can be expressed in these coordinates by: $${\displaystyle {\begin{aligned}Rf(\alpha ,s)&=\int _{-\infty }^{\infty }f(x(z),y(z))\,dz\\&=\int _{-\infty }^{\infty }f{\big (}(z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ){\big )}\,dz.\end{aligned}}}$$More generally, in the ${\displaystyle n}$-dimensional Euclidean space ${\displaystyle \mathbb {R} ^{n}}$, the Radon transform of a function ${\displaystyle f}$ satisfying the regularity conditions is a function ${\displaystyle Rf}$ on the space ${\displaystyle \Sigma _{n}}$ of all hyperplanes in ${\displaystyle \mathbb {R} ^{n}}$. It is defined by:

Shepp Logan phantom

Radon transform

Inverse Radon transform

$${\displaystyle Rf(\xi )=\int _{\xi }f(\mathbf {x} )\,d\sigma (\mathbf {x} ),\quad \forall \xi \in \Sigma _{n}}$$where the integral is taken with respect to the natural hypersurface measure, ${\displaystyle d\sigma }$ (generalizing the ${\displaystyle \vert d\mathbf {x} \vert }$ term from the ${\displaystyle 2}$-dimensional case). Observe that any element of ${\displaystyle }$Zdroj:https://en.wikipedia.org?pojem=Radon_transform
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.