This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Rhumb line" – news · newspapers · books · scholar · JSTOR (August 2017) (Learn how and when to remove this message)

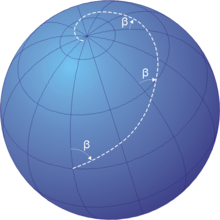
In navigation, a rhumb line, rhumb (/rʌm/), or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north.

Introduction

The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese mathematician Pedro Nunes in 1537, in his Treatise in Defense of the Marine Chart, with further mathematical development by Thomas Harriot in the 1590s.

A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature, whereas a rhumb line has non-zero geodesic curvature.

Meridians of longitude and parallels of latitude provide special cases of the rhumb line, where their angles of intersection are respectively 0° and 90°. On a north–south passage the rhumb line course coincides with a great circle, as it does on an east–west passage along the equator.

On a Mercator projection map, any rhumb line is a straight line; a rhumb line can be drawn on such a map between any two points on Earth without going off the edge of the map. But theoretically a loxodrome can extend beyond the right edge of the map, where it then continues at the left edge with the same slope (assuming that the map covers exactly 360 degrees of longitude).

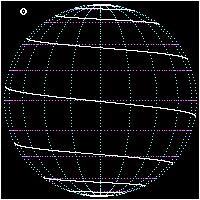
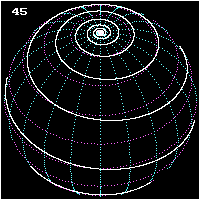
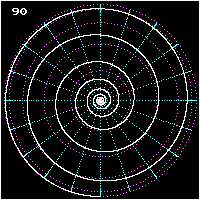
Rhumb lines which cut meridians at oblique angles are loxodromic curves which spiral towards the poles.^[1] On a Mercator projection the north and south poles occur at infinity and are therefore never shown. However the full loxodrome on an infinitely high map would consist of infinitely many line segments between the two edges. On a stereographic projection map, a loxodrome is an equiangular spiral whose center is the north or south pole.

All loxodromes spiral from one pole to the other. Near the poles, they are close to being logarithmic spirals (which they are exactly on a stereographic projection, see below), so they wind around each pole an infinite number of times but reach the pole in a finite distance. The pole-to-pole length of a loxodrome (assuming a perfect sphere) is the length of the meridian divided by the cosine of the bearing away from true north. Loxodromes are not defined at the poles.

• Three views of a pole-to-pole loxodrome
• 
• 
• 

Etymology and historical description

The word loxodrome comes from Ancient Greek λοξός loxós: "oblique" + δρόμος drómos: "running" (from δραμεῖν drameîn: "to run"). The word rhumb may come from Spanish or Portuguese rumbo/rumo ("course" or "direction") and Greek ῥόμβος rhómbos,^[2] from rhémbein.

The 1878 edition of The Globe Encyclopaedia of Universal Information describes a loxodrome line as:^[3]

Loxodrom′ic Line is a curve which cuts every member of a system of lines of curvature of a given surface at the same angle. A ship sailing towards the same point of the compass describes such a line which cuts all the meridians at the same angle. In Mercator's Projection (q.v.) the Loxodromic lines are evidently straight.^[3]

A misunderstanding could arise because the term "rhumb" had no precise meaning when it came into use. It applied equally well to the windrose lines as it did to loxodromes because the term only applied "locally" and only meant whatever a sailor did in order to sail with constant bearing, with all the imprecision that that implies. Therefore, "rhumb" was applicable to the straight lines on portolans when portolans were in use, as well as always applicable to straight lines on Mercator charts. For short distances portolan "rhumbs" do not meaningfully differ from Mercator rhumbs, but these days "rhumb" is synonymous with the mathematically precise "loxodrome" because it has been made synonymous retrospectively.

As Leo Bagrow states:^[4] "the word ('Rhumbline') is wrongly applied to the sea-charts of this period, since a loxodrome gives an accurate course only when the chart is drawn on a suitable projection. Cartometric investigation has revealed that no projection was used in the early charts, for which we therefore retain the name 'portolan'."

Mathematical description

For a sphere of radius 1, the azimuthal angle λ, the polar angle −π/2 ≤ φ ≤ π/2 (defined here to correspond to latitude), and Cartesian unit vectors i, j, and k can be used to write the radius vector r as

${\displaystyle \mathbf {r} (\lambda ,\varphi )=(\cos {\lambda }\cdot \cos {\varphi })\mathbf {i} +(\sin {\lambda }\cdot \cos {\varphi })\mathbf {j} +(\sin {\varphi })\mathbf {k} \,.}$

Orthogonal unit vectors in the azimuthal and polar directions of the sphere can be written

${\displaystyle {\begin{aligned}{\boldsymbol {\hat {\lambda }}}(\lambda ,\varphi )&=\sec {\varphi }{\frac {\partial \mathbf {r} }{\partial \lambda }}=(-\sin {\lambda })\mathbf {i} +(\cos {\lambda })\mathbf {j} \,,\\{\boldsymbol {\hat {\varphi }}}(\lambda ,\varphi )&={\frac {\partial \mathbf {r} }{\partial \varphi }}=(-\cos {\lambda }\cdot \sin {\varphi })\mathbf {i} +(-\sin {\lambda }\cdot \sin {\varphi })\mathbf {j} +(\cos {\varphi })\mathbf {k} \,,\end{aligned}}}$

which have the scalar products

${\displaystyle {\boldsymbol {\hat {\lambda }}}\cdot {\boldsymbol {\hat {\varphi }}}={\boldsymbol {\hat {\lambda }}}\cdot \mathbf {r} ={\boldsymbol {\hat {\varphi }}}\cdot \mathbf {r} =0\,.}$

λ̂ for constant φ traces out a parallel of latitude, while φ̂ for constant λ traces out a meridian of longitude, and together they generate a plane tangent to the sphere.

The unit vector

${\displaystyle \mathbf {\boldsymbol {\hat {\beta }}} (\lambda ,\varphi )=(\sin {\beta }){\boldsymbol {\hat {\lambda }}}+(\cos {\beta }){\boldsymbol {\hat {\varphi }}}}$

has a constant angle β with the unit vector φ̂ for any λ and φ, since their scalar product is

${\displaystyle {\boldsymbol {\hat {\beta }}}\cdot {\boldsymbol {\hat {\varphi }}}=\cos {\beta }\,.}$

A loxodrome is defined as a curve on the sphere that has a constant angle β with all meridians of longitude, and therefore must be parallel to the unit vector β̂. As a result, a differential length ds along the loxodrome will produce a differential displacement

Zdroj:https://en.wikipedia.org?pojem=Rhumb_line
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---