Spectral density

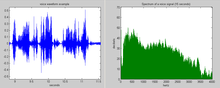
In signal processing, the power spectrum $S_{xx}(f)$ of a continuous time signal $x(t)$ describes the distribution of power into frequency components $f$ composing that signal.^[1] According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum.

When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over all time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would be found per unit time, since the total energy of such a signal over all time would generally be infinite. Summation or integration of the spectral components yields the total power (for a physical process) or variance (in a statistical process), identical to what would be obtained by integrating $x^{2}(t)$ over the time domain, as dictated by Parseval's theorem.^[1]

The spectrum of a physical process $x(t)$ often contains essential information about the nature of $x$ . For instance, the pitch and timbre of a musical instrument are immediately determined from a spectral analysis. The color of a light source is determined by the spectrum of the electromagnetic wave's electric field $E(t)$ as it fluctuates at an extremely high frequency. Obtaining a spectrum from time series such as these involves the Fourier transform, and generalizations based on Fourier analysis. In many cases the time domain is not specifically employed in practice, such as when a dispersive prism is used to obtain a spectrum of light in a spectrograph, or when a sound is perceived through its effect on the auditory receptors of the inner ear, each of which is sensitive to a particular frequency.

However this article concentrates on situations in which the time series is known (at least in a statistical sense) or directly measured (such as by a microphone sampled by a computer). The power spectrum is important in statistical signal processing and in the statistical study of stochastic processes, as well as in many other branches of physics and engineering. Typically the process is a function of time, but one can similarly discuss data in the spatial domain being decomposed in terms of spatial frequency.^[1]

Units

In physics, the signal might be a wave, such as an electromagnetic wave, an acoustic wave, or the vibration of a mechanism. The power spectral density (PSD) of the signal describes the power present in the signal as a function of frequency, per unit frequency. Power spectral density is commonly expressed in watts per hertz (W/Hz).^[2]

When a signal is defined in terms only of a voltage, for instance, there is no unique power associated with the stated amplitude. In this case "power" is simply reckoned in terms of the square of the signal, as this would always be proportional to the actual power delivered by that signal into a given impedance. So one might use units of V² Hz⁻¹ for the PSD. Energy spectral density (ESD) would have units of V² s Hz⁻¹, since energy has units of power multiplied by time (e.g., watt-hour).^[3]

In the general case, the units of PSD will be the ratio of units of variance per unit of frequency; so, for example, a series of displacement values (in meters) over time (in seconds) will have PSD in units of meters squared per hertz, m²/Hz. In the analysis of random vibrations, units of g² Hz⁻¹ are frequently used for the PSD of acceleration, where g denotes the g-force.^[4]

Mathematically, it is not necessary to assign physical dimensions to the signal or to the independent variable. In the following discussion the meaning of x(t) will remain unspecified, but the independent variable will be assumed to be that of time.

Definition

Energy spectral density

Energy spectral density describes how the energy of a signal or a time series is distributed with frequency. Here, the term energy is used in the generalized sense of signal processing;^[5] that is, the energy $E$ of a signal $x(t)$ is:

E\triangleq \int _{-\infty }^{\infty }\left|x(t)\right|^{2}\ dt.

The energy spectral density is most suitable for transients—that is, pulse-like signals—having a finite total energy. Finite or not, Parseval's theorem^[6] (or Plancherel's theorem) gives us an alternate expression for the energy of the signal:

\int _{-\infty }^{\infty }|x(t)|^{2}\,dt=\int _{-\infty }^{\infty }\left|{\hat {x}}(f)\right|^{2}\,df,

where:

{\hat {x}}(f)\triangleq \int _{-\infty }^{\infty }e^{-i2\pi ft}x(t)\ dt

is the value of the Fourier transform of

x(t)

at frequency

f

(in Hz). The theorem also holds true in the discrete-time cases. Since the integral on the left-hand side is the energy of the signal, the value of

\left|{\hat {x}}(f)\right|^{2}df

can be interpreted as a density function multiplied by an infinitesimally small frequency interval, describing the energy contained in the signal at frequency

f

in the frequency interval

f+df

.

Therefore, the energy spectral density of $x(t)$ is defined as:^[6]

{\bar {S}}_{xx}(f)\triangleq \left|{\hat {x}}(f)\right|^{2}

(Eq.1)

The function ${\bar {S}}_{xx}(f)$ and the autocorrelation of $x(t)$ form a Fourier transform pair, a result also known as the Wiener–Khinchin theorem (see also Periodogram).

As a physical example of how one might measure the energy spectral density of a signal, suppose $V(t)$ represents the potential (in volts) of an electrical pulse propagating along a transmission line of impedance $Z$ , and suppose the line is terminated with a matched resistor (so that all of the pulse energy is delivered to the resistor and none is reflected back). By Ohm's law, the power delivered to the resistor at time $t$ is equal to $V(t)^{2}/Z$ , so the total energy is found by integrating $V(t)^{2}/Z$ with respect to time over the duration of the pulse. To find the value of the energy spectral density ${\bar {S}}_{xx}(f)$ at frequency $f$ , one could insert between the transmission line and the resistor a bandpass filter which passes only a narrow range of frequencies ( $\Delta f$ , say) near the frequency of interest and then measure the total energy $E(f)$ dissipated across the resistor. The value of the energy spectral density at $f$ is then estimated to be $E(f)/\Delta f$ . In this example, since the power $V(t)^{2}/Z$ has units of V² Ω⁻¹, the energy $E(f)$ has units of V² s Ω⁻¹ = J, and hence the estimate $E(f)/\Delta f$ of the energy spectral density has units of J Hz⁻¹, as required. In many situations, it is common to forget the step of dividing by $Z$ so that the energy spectral density instead has units of V² Hz⁻¹.