Thermodynamics
The classical Carnot heat engine
Branches Classical Statistical Chemical Quantum thermodynamics Equilibrium / Non-equilibrium
Laws Zeroth First Second Third
Systems Closed system Open system Isolated system State Equation of state Ideal gas Real gas State of matter Phase (matter) Equilibrium Control volume Instruments Processes Isobaric Isochoric Isothermal Adiabatic Isentropic Isenthalpic Quasistatic Polytropic Free expansion Reversibility Irreversibility Endoreversibility Cycles Heat engines Heat pumps Thermal efficiency
System properties Note: Conjugate variables in italics Property diagrams Intensive and extensive properties Process functions Work Heat Functions of state Temperature / Entropy (introduction) Pressure / Volume Chemical potential / Particle number Vapor quality Reduced properties
Material properties Property databases Specific heat capacity  ${\displaystyle c=}$ ${\displaystyle T}$ ${\displaystyle \partial S}$ ${\displaystyle N}$ ${\displaystyle \partial T}$ Compressibility  ${\displaystyle \beta =-}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial p}$ Thermal expansion  ${\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial T}$
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Onsager reciprocal relations Bridgman's equations Table of thermodynamic equations
Potentials Free energy Free entropy Internal energy ${\displaystyle U(S,V)}$ Enthalpy ${\displaystyle H(S,p)=U+pV}$ Helmholtz free energy ${\displaystyle A(T,V)=U-TS}$ Gibbs free energy ${\displaystyle G(T,p)=H-TS}$
History Culture History General Entropy Gas laws "Perpetual motion" machines Philosophy Entropy and time Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics Theories Caloric theory Vis viva ("living force") Mechanical equivalent of heat Motive power Key publications An Experimental Enquiry Concerning ... Heat On the Equilibrium of Heterogeneous Substances Reflections on the Motive Power of Fire Timelines Thermodynamics Heat engines Art Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Boltzmann Bridgman Carathéodory Carnot Clapeyron Clausius de Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

An adiabatic process (adiabatic from Ancient Greek ἀδιάβατος (adiábatos) 'impassable') is a type of thermodynamic process that occurs without transferring heat or mass between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work.^[1][2] As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is diabatic.

Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".^[3] For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of flame temperature by assuming combustion loses no heat to its surroundings.

In meteorology, adiabatic expansion and cooling of moist air, which can be triggered by winds flowing up and over a mountain for example, can cause the water vapor pressure to exceed the saturation vapor pressure. Expansion and cooling beyond the saturation vapor pressure is often idealized as a pseudo-adiabatic process whereby excess vapor instantaneously precipitates into water droplets. The change in temperature of an air undergoing pseudo-adiabatic expansion differs from air undergoing adiabatic expansion because latent heat is released by precipitation.^[4]

Description

A process without transfer of heat to or from a system, so that Q = 0, is called adiabatic, and such a system is said to be adiabatically isolated.^[5][6] The simplifying assumption frequently made is that a process is adiabatic. For example, the compression of a gas within a cylinder of an engine is assumed to occur so rapidly that on the time scale of the compression process, little of the system's energy can be transferred out as heat to the surroundings. Even though the cylinders are not insulated and are quite conductive, that process is idealized to be adiabatic. The same can be said to be true for the expansion process of such a system.

The assumption of adiabatic isolation is useful and often combined with other such idealizations to calculate a good first approximation of a system's behaviour. For example, according to Laplace, when sound travels in a gas, there is no time for heat conduction in the medium, and so the propagation of sound is adiabatic. For such an adiabatic process, the modulus of elasticity (Young's modulus) can be expressed as E = γP, where γ is the ratio of specific heats at constant pressure and at constant volume (γ = C_p/C_v) and P is the pressure of the gas.

Various applications of the adiabatic assumption

For a closed system, one may write the first law of thermodynamics as ΔU = Q − W, where ΔU denotes the change of the system's internal energy, Q the quantity of energy added to it as heat, and W the work done by the system on its surroundings.

• If the system has such rigid walls that work cannot be transferred in or out (W = 0), and the walls are not adiabatic and energy is added in the form of heat (Q > 0), and there is no phase change, then the temperature of the system will rise.
• If the system has such rigid walls that pressure–volume work cannot be done, but the walls are adiabatic (Q = 0), and energy is added as isochoric (constant volume) work in the form of friction or the stirring of a viscous fluid within the system (W < 0), and there is no phase change, then the temperature of the system will rise.
• If the system walls are adiabatic (Q = 0) but not rigid (W ≠ 0), and, in a fictive idealized process, energy is added to the system in the form of frictionless, non-viscous pressure–volume work (W < 0), and there is no phase change, then the temperature of the system will rise. Such a process is said to be "reversible". Ideally, if the process were reversed the energy could be recovered entirely as work done by the system. Should the work be added in such a way that friction or viscous forces are operating within the system, and if there is no phase change, then the temperature of the system will rise, the process is said to be "irreversible", and the work added to the system is not entirely recoverable in the form of work.
• If the walls of a system are not adiabatic, and energy is transferred in as heat, the process is not adiabatic, having Q > 0, and ΔS > 0 according to the second law of thermodynamics.

Naturally occurring adiabatic processes are irreversible.

The transfer of energy as work into an adiabatically isolated system can be imagined as being of two idealized extreme kinds. In one such kind, no friction, viscous dissipation, etc., and the work is only pressure-volume work (denoted by P dV). In nature, this ideal kind occurs only approximately because it demands an infinitely slow process and no sources of dissipation.

The other extreme kind of work is isochoric work (dV = 0), for which energy is added as work solely through friction or viscous dissipation within the system. A stirrer that transfers energy to a viscous fluid of an adiabatically isolated system with rigid walls, without phase change, will cause a rise in temperature of the fluid, but that work is not recoverable. Isochoric work is irreversible.^[7] The second law of thermodynamics observes that a natural process, of transfer of energy as work, always consists at least of isochoric work and often both of these extreme kinds of work. Every natural process, adiabatic or not, is irreversible, with ΔS > 0, as friction or viscosity are always present to some extent.

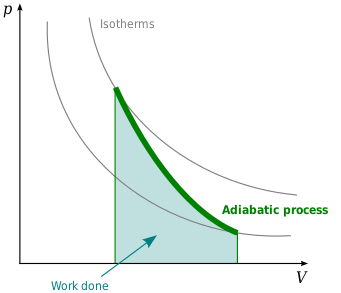
Adiabatic compression and expansion

The adiabatic compression of a gas causes a rise in temperature of the gas. Adiabatic expansion against pressure, or a spring, causes a drop in temperature. In contrast, free expansion is an isothermal process for an ideal gas.

Adiabatic compression occurs when the pressure of a gas is increased by work done on it by its surroundings, e.g., a piston compressing a gas contained within a cylinder and raising the temperature where in many practical situations heat conduction through walls can be slow compared with the compression time. This finds practical application in diesel engines which rely on the lack of heat dissipation during the compression stroke to elevate the fuel vapor temperature sufficiently to ignite it.

Adiabatic compression occurs in the Earth's atmosphere when an air mass descends, for example, in a Katabatic wind, Foehn wind, or Chinook wind flowing downhill over a mountain range. When a parcel of air descends, the pressure on the parcel increases. Because of this increase in pressure, the parcel's volume decreases and its temperature increases as work is done on the parcel of air, thus increasing its internal energy, which manifests itself by a rise in the temperature of that mass of air. The parcel of air can only slowly dissipate the energy by conduction or radiation (heat), and to a first approximation it can be considered adiabatically isolated and the process an adiabatic process.

Adiabatic expansion occurs when the pressure on an adiabatically isolated system is decreased, allowing it to expand in size, thus causing it to do work on its surroundings. When the pressure applied on a parcel of gas is reduced, the gas in the parcel is allowed to expand; as the volume increases, the temperature falls as its internal energy decreases. Adiabatic expansion occurs in the Earth's atmosphere with orographic lifting and lee waves, and this can form pilei or lenticular clouds.

Due in part to adiabatic expansion in mountainous areas, snowfall infrequently occurs in some parts of the Sahara desert.^[8]

Adiabatic expansion does not have to involve a fluid. One technique used to reach very low temperatures (thousandths and even millionths of a degree above absolute zero) is via adiabatic demagnetisation, where the change in magnetic field on a magnetic material is used to provide adiabatic expansion. Also, the contents of an expanding universe can be described (to first order) as an adiabatically expanding fluid. (See heat death of the universe.)

Rising magma also undergoes adiabatic expansion before eruption, particularly significant in the case of magmas that rise quickly from great depths such as kimberlites.^[9]

In the Earth's convecting mantle (the asthenosphere) beneath the lithosphere, the mantle temperature is approximately an adiabat. The slight decrease in temperature with shallowing depth is due to the decrease in pressure the shallower the material is in the Earth.^[10]

Such temperature changes can be quantified using the ideal gas law, or the hydrostatic equation for atmospheric processes.

In practice, no process is truly adiabatic. Many processes rely on a large difference in time scales of the process of interest and the rate of heat dissipation across a system boundary, and thus are approximated by using an adiabatic assumption. There is always some heat loss, as no perfect insulators exist.

Ideal gas (reversible process)

The mathematical equation for an ideal gas undergoing a reversible adiabatic process can be represented by the polytropic process equation^[3]

${\displaystyle PV^{\gamma }={\text{constant}},}$

where P is pressure, V is volume, and γ is the adiabatic index or heat capacity ratio defined as

${\displaystyle \gamma ={\frac {C_{P}}{C_{V}}}={\frac {f+2}{f}}.}$

Here C_P is the specific heat for constant pressure, C_V is the specific heat for constant volume, and f is the number of degrees of freedom (3 for a monatomic gas, 5 for a diatomic gas or a gas of linear molecules such as carbon dioxide).

For a monatomic ideal gas, γ = 5/3, and for a diatomic gas (such as nitrogen and oxygen, the main components of air), γ = 7/5.^[11] Note that the above formula is only applicable to classical ideal gases (that is, gases far above absolute zero temperature) and not Bose–Einstein or Fermi gases.

One can also use the ideal gas law to rewrite the above relationship between P and V as ^[3]

${\displaystyle P^{1-\gamma }T^{\gamma }={\text{constant}},}$

${\displaystyle TV^{\gamma -1}={\text{constant}}.}$

where T is the absolute or thermodynamic temperature.

Example of adiabatic compression

The compression stroke in a gasoline engine can be used as an example of adiabatic compression. The model assumptions are: the uncompressed volume of the cylinder is one litre (1 L = 1000 cm³ = 0.001 m³); the gas within is the air consisting of molecular nitrogen and oxygen only (thus a diatomic gas with 5 degrees of freedom, and so γ = 7/5); the compression ratio of the engine is 10:1 (that is, the 1 L volume of uncompressed gas is reduced to 0.1 L by the piston); and the uncompressed gas is at approximately room temperature and pressure (a warm room temperature of ~27 °C, or 300 K, and a pressure of 1 bar = 100 kPa, i.e. typical sea-level atmospheric pressure).

Zdroj:https://en.wikipedia.org?pojem=Adiabatic
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---