This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2011) (Learn how and when to remove this message)

Part of a series on
Bayesian statistics
Posterior = Likelihood × Prior ÷ Evidence
Background
Bayesian inference Bayesian probability Bayes' theorem Bernstein–von Mises theorem Coherence Cox's theorem Cromwell's rule Principle of indifference Principle of maximum entropy
Model building
Weak prior ... Strong prior Conjugate prior Linear regression Empirical Bayes Hierarchical model
Posterior approximation
Markov chain Monte Carlo Laplace's approximation Integrated nested Laplace approximations Variational inference Approximate Bayesian computation
Estimators
Bayesian estimator Credible interval Maximum a posteriori estimation
Evidence approximation
Evidence lower bound Nested sampling
Model evaluation
Bayes factor Model averaging Posterior predictive
Mathematics portal
v t e

A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG).^[1] While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g. speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.

Graphical model

Formally, Bayesian networks are directed acyclic graphs (DAGs) whose nodes represent variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Each edge represents a direct conditional dependency. Any pair of nodes that are not connected (i.e. no path connects one node to the other) represent variables that are conditionally independent of each other. Each node is associated with a probability function that takes, as input, a particular set of values for the node's parent variables, and gives (as output) the probability (or probability distribution, if applicable) of the variable represented by the node. For example, if ${\displaystyle m}$ parent nodes represent ${\displaystyle m}$ Boolean variables, then the probability function could be represented by a table of ${\displaystyle 2^{m}}$ entries, one entry for each of the ${\displaystyle 2^{m}}$ possible parent combinations. Similar ideas may be applied to undirected, and possibly cyclic, graphs such as Markov networks.

Example

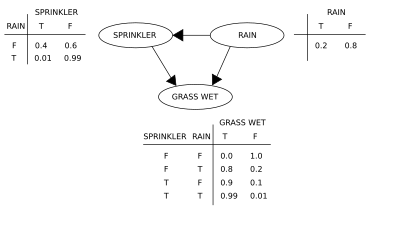
Let us use an illustration to enforce the concepts of a Bayesian network. Suppose we want to model the dependencies between three variables: the sprinkler (or more appropriately, its state - whether it is on or not), the presence or absence of rain and whether the grass is wet or not. Observe that two events can cause the grass to become wet: an active sprinkler or rain. Rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler usually is not active). This situation can be modeled with a Bayesian network (shown to the right). Each variable has two possible values, T (for true) and F (for false).

The joint probability function is, by the chain rule of probability,

${\displaystyle \Pr(G,S,R)=\Pr(G\mid S,R)\Pr(S\mid R)\Pr(R)}$

where G = "Grass wet (true/false)", S = "Sprinkler turned on (true/false)", and R = "Raining (true/false)".

The model can answer questions about the presence of a cause given the presence of an effect (so-called inverse probability) like "What is the probability that it is raining, given the grass is wet?" by using the conditional probability formula and summing over all nuisance variables:

${\displaystyle \Pr(R=T\mid G=T)={\frac {\Pr(G=T,R=T)}{\Pr(G=T)}}={\frac {\sum _{x\in \{T,F\}}\Pr(G=T,S=x,R=T)}{\sum _{x,y\in \{T,F\}}\Pr(G=T,S=x,R=y)}}}$

Using the expansion for the joint probability function ${\displaystyle \Pr(G,S,R)}$ and the conditional probabilities from the conditional probability tables (CPTs) stated in the diagram, one can evaluate each term in the sums in the numerator and denominator. For example,

${\displaystyle {\begin{aligned}\Pr(G=T,S=T,R=T)&=\Pr(G=T\mid S=T,R=T)\Pr(S=T\mid R=T)\Pr(R=T)\\&=0.99\times 0.01\times 0.2\\&=0.00198.\end{aligned}}}$

Then the numerical results (subscripted by the associated variable values) are

${\displaystyle \Pr(R=T\mid G=T)={\frac {0.00198_{TTT}+0.1584_{TFT}}{0.00198_{TTT}+0.288_{TTF}+0.1584_{TFT}+0.0_{TFF}}}={\frac {891}{2491}}\approx 35.77\%.}$

To answer an interventional question, such as "What is the probability that it would rain, given that we wet the grass?" the answer is governed by the post-intervention joint distribution function

${\displaystyle \Pr(S,R\mid {\text{do}}(G=T))=\Pr(S\mid R)\Pr(R)}$

obtained by removing the factor ${\displaystyle \Pr(G\mid S,R)}$ from the pre-intervention distribution. The do operator forces the value of G to be true. The probability of rain is unaffected by the action:

${\displaystyle \Pr(R\mid {\text{do}}(G=T))=\Pr(R).}$

To predict the impact of turning the sprinkler on:

${\displaystyle Pr(R,G\mid <!--\; \mid \; -->\text{do}(S=}$Zdroj:https://en.wikipedia.org?pojem=Bayesian_network
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---