The black hole information paradox^[1] is a paradox that appears when the predictions of quantum mechanics and general relativity are combined. The theory of general relativity predicts the existence of black holes that are regions of spacetime from which nothing—not even light—can escape. In the 1970s, Stephen Hawking applied the semiclassical approach of quantum field theory in curved spacetime to such systems and found that an isolated black hole would emit a form of radiation (now called Hawking radiation in his honor). He also argued that the detailed form of the radiation would be independent of the initial state of the black hole,^[2] and depend only on its mass, electric charge and angular momentum.

The information paradox appears when one considers a process in which a black hole is formed through a physical process and then evaporates away entirely through Hawking radiation. Hawking's calculation suggests that the final state of radiation would retain information only about the total mass, electric charge and angular momentum of the initial state. Since many different states can have the same mass, charge and angular momentum, this suggests that many initial physical states could evolve into the same final state. Therefore, information about the details of the initial state would be permanently lost; however, this violates a core precept of both classical and quantum physics: that, in principle, the state of a system at one point in time should determine its state at any other time.^[3][4] Specifically, in quantum mechanics the state of the system is encoded by its wave function. The evolution of the wave function is determined by a unitary operator, and unitarity implies that the wave function at any instant of time can be used to determine the wave function either in the past or the future. In 1993, Don Page argued that if a black hole starts in a pure quantum state and evaporates completely by a unitary process, the von Neumann entropy of the Hawking radiation initially increases and then decreases back to zero when the black hole has disappeared.^[5] This is called the Page curve.^[6]

It is now generally believed that information is preserved in black-hole evaporation.^[7][8][9] For many researchers, deriving the Page curve is synonymous with solving the black hole information puzzle.^[10]: 291 But views differ as to precisely how Hawking's original semiclassical calculation should be corrected.^{[8][9][11][12]} In recent years, several extensions of the original paradox have been explored. Taken together, these puzzles about black hole evaporation have implications for how gravity and quantum mechanics must be combined. The information paradox remains an active field of research in quantum gravity.

Relevant principles

In quantum mechanics, the evolution of the state is governed by the Schrödinger equation. The Schrödinger equation obeys two principles that are relevant to the paradox—quantum determinism, which means that given a present wave function, its future changes are uniquely determined by the evolution operator, and reversibility, which refers to the fact that the evolution operator has an inverse, meaning that the past wave functions are similarly unique. The combination of the two means that information must always be preserved.^[13] In this context "information" means all the details of the state, and the statement that information must be preserved means that details corresponding to an earlier time can always be reconstructed at a later time.

Mathematically, the Schrödinger equation implies that the wavefunction at a time t₁ can be related to the wavefunction at a time t₂ by means of a unitary operator.

Since the unitary operator is bijective, the wavefunction at t₂ can be obtained from the wavefunction at t₁ and vice versa.

The reversibility of time evolution described above applies only at the microscopic level, since the wavefunction provides a complete description of the state. It should not be conflated with thermodynamic irreversibility. A process may appear irreversible if one keeps track only of the system's coarse-grained features and not of its microscopic details, as is usually done in thermodynamics. But at the microscopic level, the principles of quantum mechanics imply that every process is completely reversible.

Starting in the mid-1970s, Stephen Hawking and Jacob Bekenstein put forward theoretical arguments that suggested that black-hole evaporation loses information, and is therefore inconsistent with unitarity. Crucially, these arguments were meant to apply at the microscopic level and suggested that black-hole evaporation is not only thermodynamically but microscopically irreversible. This contradicts the principle of unitarity described above and leads to the information paradox. Since the paradox suggested that quantum mechanics would be violated by black-hole formation and evaporation, Hawking framed the paradox in terms of the "breakdown of predictability in gravitational collapse".^[2]

The arguments for microscopic irreversibility were backed by Hawking's calculation of the spectrum of radiation that isolated black holes emit.^[14] This calculation utilized the framework of general relativity and quantum field theory. The calculation of Hawking radiation is performed at the black hole horizon and does not account for the backreaction of spacetime geometry; for a large enough black hole the curvature at the horizon is small and therefore both these theories should be valid. Hawking relied on the no-hair theorem to arrive at the conclusion that radiation emitted by black holes would depend only on a few macroscopic parameters, such as the black hole's mass, charge, and spin, but not on the details of the initial state that led to the formation of the black hole. In addition, the argument for information loss relied on the causal structure of the black hole spacetime, which suggests that information in the interior should not affect any observation in the exterior, including observations performed on the radiation the black hole emits. If so, the region of spacetime outside the black hole would lose information about the state of the interior after black-hole evaporation, leading to the loss of information.

Today, some physicists believe that the holographic principle (specifically the AdS/CFT duality) demonstrates that Hawking's conclusion was incorrect, and that information is in fact preserved.^[15] Moreover, recent analyses indicate that in semiclassical gravity the information loss paradox cannot be formulated in a self-consistent manner due to the impossibility of simultaneously realizing all of the necessary assumptions required for its formulation.^[16][17]

Black hole evaporation

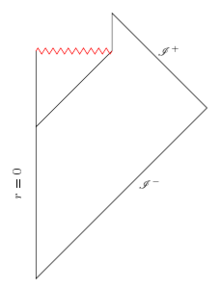
In 1973–1975, Stephen Hawking showed that black holes should slowly radiate away energy, and he later argued that this leads to a contradiction with unitarity. Hawking used the classical no-hair theorem to argue that the form of this radiation—called Hawking radiation—would be completely independent of the initial state of the star or matter that collapsed to form the black hole. He argued that the process of radiation would continue until the black hole had evaporated completely. At the end of this process, all the initial energy in the black hole would have been transferred to the radiation. But, according to Hawking's argument, the radiation would retain no information about the initial state and therefore information about the initial state would be lost.

More specifically, Hawking argued that the pattern of radiation emitted from the black hole would be random, with a probability distribution controlled only by the black hole's initial temperature, charge, and angular momentum, not by the initial state of the collapse. The state produced by such a probabilistic process is called a mixed state in quantum mechanics. Therefore, Hawking argued that if the star or material that collapsed to form the black hole started in a specific pure quantum state, the process of evaporation would transform the pure state into a mixed state. This is inconsistent with the unitarity of quantum-mechanical evolution discussed above.

The loss of information can be quantified in terms of the change in the fine-grained von Neumann entropy of the state. A pure state is assigned a von Neumann entropy of 0, whereas a mixed state has a finite entropy. The unitary evolution of a state according to Schrödinger's equation preserves the entropy. Therefore Hawking's argument suggests that the process of black-hole evaporation cannot be described within the framework of unitary evolution. Although this paradox is often phrased in terms of quantum mechanics, the evolution from a pure state to a mixed state is also inconsistent with Liouville's theorem in classical physics (see e.g.^[18]).

In equations, Hawking showed that if one denotes the creation and annihilation operators at a frequency ${\displaystyle \omega }$ for a quantum field propagating in the black-hole background by ${\displaystyle a_{\omega }}$ and ${\displaystyle a_{\omega }^{\dagger }}$ then the expectation value of the product of these operators in the state formed by the collapse of a black hole would satisfy

where k is the Boltzmann constant and T is the temperature of the black hole. (See, for example, section 2.2 of.^[9]) This formula has two important aspects. The first is that the form of the radiation depends only on a single parameter, temperature, even though the initial state of the black hole cannot be characterized by one parameter. Second, the formula implies that the black hole radiates mass at a rate given by where a is constant related to fundamental constants, including the Stefan–Boltzmann constant and certain properties of the black hole spacetime called its greybody factors.

The temperature of the black hole is in turn dependent on its mass, charge, and angular momentum. For a Schwarzschild black hole the temperature is given by

This means that if the black hole starts out with an initial mass ${\displaystyle M_{0}}$, it evaporates completely in a time proportional to ${\displaystyle M_{0}^{3}}$.

The important aspect of these formulas is that they suggest that the final gas of radiation formed through this process depends only on the black hole's temperature and is independent of other details of the initial state. This leads to the following paradox. Consider two distinct initial states that collapse to form a Schwarzschild black hole of the same mass. Even though the states were distinct at first, since the mass (and hence the temperature) of the black holes is the same, they will emit the same Hawking radiation. Once they evaporate completely, in both cases, one will be left with a featureless gas of radiation. This gas cannot be used to distinguish between the two initial states, and therefore information has been lost.

It is now widely believed that the reasoning leading to the paradox above is flawed. Several solutions are reviewed below.

Popular culture

The information paradox has received coverage in the popular media and has been described in popular-science books. Some of this coverage resulted from a widely publicized bet made in 1997 between John Preskill on the one hand with Hawking and Kip Thorne on the other that information was not lost in black holes. The scientific debate on the paradox was described in Leonard Susskind's 2008 book The Black Hole War. (The book carefully notes that the 'war' was purely a scientific one, and that, at a personal level, the participants remained friends.^[19]) Susskind writes that Hawking was eventually persuaded that black-hole evaporation was unitary by the holographic principle, which was first proposed by 't Hooft, further developed by Susskind, and later given a precise string theory interpretation by the AdS/CFT correspondence.^[20] In 2004, Hawking also conceded the 1997 bet, paying Preskill with a baseball encyclopedia "from which information can be retrieved at will". Thorne refused to concede.^[21]

Solutions

Since the 1997 proposal of the AdS/CFT correspondence, the predominant belief among physicists is that information is indeed preserved in black hole evaporation. There are broadly two main streams of thought about how this happens. Within what might broadly be termed the "string theory community", the dominant idea is that Hawking radiation is not precisely thermal but receives quantum correlations that encode information about the black hole's interior.^[9] This viewpoint has been the subject of extensive recent research and received further support in 2019 when researchers amended the computation of the entropy of the Hawking radiation in certain models and showed that the radiation is in fact dual to the black hole interior at late times.^[22][23] Hawking himself was influenced by this view and in 2004 published a paper that assumed the AdS/CFT correspondence and argued that quantum perturbations of the event horizon could allow information to escape from a black hole, which would resolve the information paradox.^[24] In this perspective, it is the event horizon of the black hole that is important and not the black-hole singularity. The GISR (Gravity Induced Spontaneous Radiation) mechanism of references^[25][26] can be considered an implementation of this idea but with the quantum perturbations of the event horizon replaced by the microscopic states of the black hole.

On the other hand, within what might broadly be termed the "loop quantum gravity community", the dominant belief is that to resolve the information paradox, it is important to understand how the black-hole singularity is resolved. These scenarios are broadly called remnant scenarios since information does not emerge gradually but remains in the black-hole interior only to emerge at the end of black-hole evaporation.^[12]

Researchers also study other possibilities, including a modification of the laws of quantum mechanics to allow for non-unitary time evolution.

Some of these solutions are described at greater length below.

GISR mechanism resolution to the paradox

Source:^[25][26]

This resolution takes GISR as the underlying mechanism for Hawking radiation and considers the latter only as a result. The physics ingredients of GISR are reflected in the following explicitly hermitian hamiltonian

The first term of ${\displaystyle H}$ is a diagonal matrix representing the microscopic state of black holes no heavier than the initial one; The second term describes the vacuum fluctuation of particles around the black hole and is represented by many harmonic oscillators; The third term couples the vacuum fluctuation modes to the black hole so that, for each mode whose energy matches the difference between two states of the black hole, the latter transits at an amplitude proportional to the similarity factor of the two states’ microscopic wave function. Transitions from the higher energy state ${\displaystyle u}$ to lower one ${\displaystyle v}$ and vice versa are equally allowed at the hamiltonian level. The form of this coupling is an imitation of the photon-atom's coupling in Jaynes–Cummings model of atomic physics. It just replaces the vector potential of the photon in JC model with the binding energy of the to be radiated particles in black hole case and the dipole moment of the initial-to-final state of the atom with the similarity factor of the black hole's initial and final state wave function. Although this form of coupling is ad hoc in a sense, it introduces no new interaction except gravitation and it must happen this way or the other no matter how the final quantum gravitation theory grows like.

From the hamiltonian of GISR and the standard Schrodinger equation controlling the evolution of wave function of the system

${\displaystyle |\mathrm{\psi <!--\; \psi \; -->}(t)⟩<!--\; ⟩\; -->=\underset{u=w}{\overset{0}{\sum <!--\; \sum \; -->}}\underset{n=1}{\overset{u}{\sum <!--\; \sum \; -->}}\underset{\mathrm{\omega <!--\; \omega \; -->}s}{\overset{\mathrm{\omega <!--\; \omega \; -->}+u=}{\sum <!--\; \sum \; -->}}}$Zdroj:https://en.wikipedia.org?pojem=Black_hole_information_loss_paradox
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---