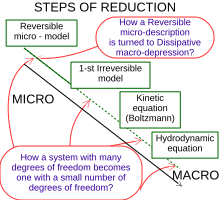
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium; it was devised by Ludwig Boltzmann in 1872.^[2] The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.

The equation arises not by analyzing the individual positions and momenta of each particle in the fluid but rather by considering a probability distribution for the position and momentum of a typical particle—that is, the probability that the particle occupies a given very small region of space (mathematically the volume element ${\displaystyle d^{3}\mathbf {r} }$) centered at the position ${\displaystyle \mathbf {r} }$, and has momentum nearly equal to a given momentum vector ${\displaystyle \mathbf {p} }$ (thus occupying a very small region of momentum space ${\displaystyle d^{3}\mathbf {p} }$), at an instant of time.

The Boltzmann equation can be used to determine how physical quantities change, such as heat energy and momentum, when a fluid is in transport. One may also derive other properties characteristic to fluids such as viscosity, thermal conductivity, and electrical conductivity (by treating the charge carriers in a material as a gas).^[2] See also convection–diffusion equation.

The equation is a nonlinear integro-differential equation, and the unknown function in the equation is a probability density function in six-dimensional space of a particle position and momentum. The problem of existence and uniqueness of solutions is still not fully resolved, but some recent results are quite promising.^[3][4]

Overview

The phase space and density function

The set of all possible positions r and momenta p is called the phase space of the system; in other words a set of three coordinates for each position coordinate x, y, z, and three more for each momentum component p_x, p_y, p_z. The entire space is 6-dimensional: a point in this space is (r, p) = (x, y, z, p_x, p_y, p_z), and each coordinate is parameterized by time t. The small volume ("differential volume element") is written

Since the probability of N molecules, which all have r and p within ${\displaystyle d^{3}\mathbf {r} \,d^{3}\mathbf {p} }$, is in question, at the heart of the equation is a quantity f which gives this probability per unit phase-space volume, or probability per unit length cubed per unit momentum cubed, at an instant of time t. This is a probability density function: f(r, p, t), defined so that,

is the number of molecules which all have positions lying within a volume element ${\displaystyle d^{3}\mathbf {r} }$ about r and momenta lying within a momentum space element ${\displaystyle d^{3}\mathbf {p} }$ about p, at time t.^[5] Integrating over a region of position space and momentum space gives the total number of particles which have positions and momenta in that region:

which is a 6-fold integral. While f is associated with a number of particles, the phase space is for one-particle (not all of them, which is usually the case with deterministic many-body systems), since only one r and p is in question. It is not part of the analysis to use r₁, p₁ for particle 1, r₂, p₂ for particle 2, etc. up to r_N, p_N for particle N.

It is assumed the particles in the system are identical (so each has an identical mass m). For a mixture of more than one chemical species, one distribution is needed for each, see below.

Principal statement

The general equation can then be written as^[6]

where the "force" term corresponds to the forces exerted on the particles by an external influence (not by the particles themselves), the "diff" term represents the diffusion of particles, and "coll" is the collision term – accounting for the forces acting between particles in collisions. Expressions for each term on the right side are provided below.^[6]

Note that some authors use the particle velocity v instead of momentum p; they are related in the definition of momentum by p = mv.

The force and diffusion terms

Consider particles described by f, each experiencing an external force F not due to other particles (see the collision term for the latter treatment).

Suppose at time t some number of particles all have position r within element ${\displaystyle d^{3}\mathbf {r} }$ and momentum p within ${\displaystyle d^{3}\mathbf {p} }$. If a force F instantly acts on each particle, then at time t + Δt their position will be ${\displaystyle \mathbf {r} +\Delta \mathbf {r} =\mathbf {r} +{\frac {\mathbf {p} }{m}}\,\Delta t}$ and momentum p + Δp = p + FΔt. Then, in the absence of collisions, f must satisfy