This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "CIE 1931 color space" – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this message)

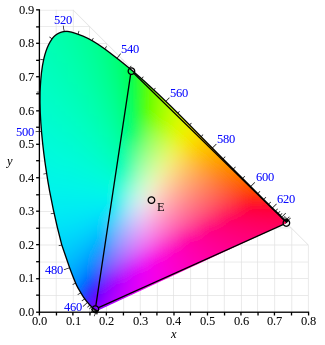
The CIE 1931 color spaces are the first defined quantitative links between distributions of wavelengths in the electromagnetic visible spectrum, and physiologically perceived colors in human color vision. The mathematical relationships that define these color spaces are essential tools for color management, important when dealing with color inks, illuminated displays, and recording devices such as digital cameras. The system was designed in 1931 by the "Commission Internationale de l'éclairage", known in English as the International Commission on Illumination.

The CIE 1931 RGB color space and CIE 1931 XYZ color space were created by the International Commission on Illumination (CIE) in 1931.^[1][2] They resulted from a series of experiments done in the late 1920s by William David Wright using ten observers^[3] and John Guild using seven observers.^[4] The experimental results were combined into the specification of the CIE RGB color space, from which the CIE XYZ color space was derived.

The CIE 1931 color spaces are still widely used, as is the 1976 CIELUV color space.

Tristimulus values

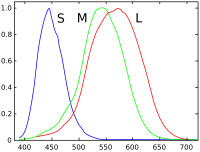
The human eye with normal vision has three kinds of cone cells that sense light, having peaks of spectral sensitivity in short ("S", 420 nm – 440 nm), medium ("M", 530 nm – 540 nm), and long ("L", 560 nm – 580 nm) wavelengths. These cone cells underlie human color perception in conditions of medium and high brightness; in very dim light color vision diminishes, and the low-brightness, monochromatic "night vision" receptors, denominated "rod cells", become effective. Thus, three parameters corresponding to levels of stimulus of the three kinds of cone cells, in principle describe any human color sensation. Weighting a total light power spectrum by the individual spectral sensitivities of the three kinds of cone cells renders three effective values of stimulus; these three values compose a tristimulus specification of the objective color of the light spectrum. The three parameters, denoted "S", "M", and "L", are indicated using a 3-dimensional space denominated the "LMS color space", which is one of many color spaces devised to quantify human color vision.

A color space maps a range of physically produced colors from mixed light, pigments, etc. to an objective description of color sensations registered in the human eye, typically in terms of tristimulus values, but not usually in the LMS color space defined by the spectral sensitivities of the cone cells. The tristimulus values associated with a color space can be conceptualized as amounts of three primary colors in a tri-chromatic, additive color model. In some color spaces, including the LMS and XYZ spaces, the primary colors used are not real colors in the sense that they cannot be generated in any light spectrum.

The CIE XYZ color space encompasses all color sensations that are visible to a person with average eyesight. That is why CIE XYZ (Tristimulus values) is a device-invariant representation of color.^[5] It serves as a standard reference against which many other color spaces are defined. A set of color-matching functions, like the spectral sensitivity curves of the LMS color space, but not restricted to non-negative sensitivities, associates physically produced light spectra with specific tristimulus values.

Consider two light sources composed of different mixtures of various wavelengths. Such light sources may appear to be the same color; this effect is called "metamerism." Such light sources have the same apparent color to an observer when they produce the same tristimulus values, regardless of the spectral power distributions of the sources.

Most wavelengths stimulate two or all three kinds of cone cell because the spectral sensitivity curves of the three kinds overlap. Certain tristimulus values are thus physically impossible: e.g. LMS tristimulus values that are non-zero for the M component and zero for both the L and S components. Furthermore pure spectral colors would, in any normal trichromatic additive color space, e.g., the RGB color spaces, imply negative values for at least one of the three primaries because the chromaticity would be outside the color triangle defined by the primary colors. To avoid these negative RGB values, and to have one component that describes the perceived brightness, "imaginary" primary colors and corresponding color-matching functions were formulated. The CIE 1931 color space defines the resulting tristimulus values, in which they are denoted by "X", "Y", and "Z".^[6] In XYZ space, all combinations of non-negative coordinates are meaningful, but many, such as the primary locations , , and , correspond to imaginary colors outside the space of possible LMS coordinates; imaginary colors do not correspond to any spectral distribution of wavelengths and therefore have no physical reality.

Meaning of X, Y and Z

In the CIE 1931 model, Y is the luminance, Z is quasi-equal to blue (of CIE RGB), and X is a mix of the three CIE RGB curves chosen to be nonnegative (see § Definition of the CIE XYZ color space). Setting Y as luminance has the useful result that for any given Y value, the XZ plane will contain all possible chromaticities at that luminance.

The unit of the tristimulus values X, Y, and Z is often arbitrarily chosen so that Y = 1 or Y = 100 is the brightest white that a color display supports. In this case, the Y value is known as the relative luminance. The corresponding whitepoint values for X and Z can then be inferred using the standard illuminants.

Since the XYZ values are defined much earlier than the characterization of cone cells in the 1950s (by Ragnar Granit),^[7] the physiological meaning of these values are known only much later. The Hunt-Pointer-Estevez matrix from the 1980s relates XYZ with LMS.^[8] When inverted, it shows how the three cone responses add up to XYZ functions:

${\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}=\left{\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\rm {HPE}}}$

In other words, the Z value is solely made up of the S cone response, the Y value a mix of L and M responses, and X value a mix of all three. This fact makes XYZ values analogous to, but different from, the LMS cone responses of the human eye.

CIE standard observer

Due to the distribution of cones in the eye, the tristimulus values depend on the observer's field of view. To eliminate this variable, the CIE defined a color-mapping function called the standard (colorimetric) observer, to represent an average human's chromatic response within a 2° arc inside the fovea. This angle was chosen owing to the belief that the color-sensitive cones resided within a 2° arc of the fovea. Thus the CIE 1931 Standard Observer function is also known as the CIE 1931 2° Standard Observer. A more modern but less-used alternative is the CIE 1964 10° Standard Observer, which is derived from the work of Stiles and Burch,^[9] and Speranskaya.^[10]

For the 10° experiments, the observers were instructed to ignore the central 2° spot. The 1964 Supplementary Standard Observer function is recommended when dealing with more than about a 4° field of view. Both standard observer functions are discretized at 5 nm wavelength intervals from 380 nm to 780 nm and distributed by the CIE.^[11] All corresponding values have been calculated from experimentally obtained data using interpolation. The standard observer is characterized by three color matching functions.

There is also a 1 nm-interval dataset of CIE 1931 and CIE 1964 provided by Wyszecki 1982.^[12] A CIE publication in 1986 appears also to have a 1 nm dataset, probably using the same data.^[13] Like the regular 5 nm dataset, this dataset is also derived from interpolation.

The derivation of the CIE standard observer from color matching experiments is given below, after the description of the CIE RGB space.

Color matching functions

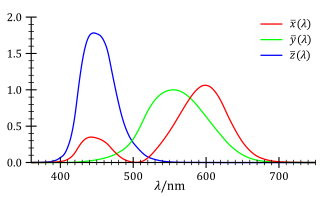
The CIE's color matching functions ${\displaystyle {\overline {x}}(\lambda )}$, ${\displaystyle {\overline {y}}(\lambda )}$ and ${\displaystyle {\overline {z}}(\lambda )}$ are the numerical description of the chromatic response of the observer (described above). They can be thought of as the spectral sensitivity curves of three linear light detectors yielding the CIE tristimulus values X, Y and Z. Collectively, these three functions describe the CIE standard observer.^[14]

Analytical approximation

Table lookup can become impractical for some computational tasks. Instead of referring to the published table, the CIE XYZ color matching functions can be approximated by a sum of Gaussian functions, as follows:^[15]

Let g(x) denote a piecewise-Gaussian function, defined by

${\displaystyle g(x;\mu ,\tau _{1},\tau _{2})={\begin{cases}\exp {\bigl (}{-\tau _{1}^{2}(x-\mu )^{2}/2}{\bigr )},&x<\mu ,\\\exp {\bigl (}{-\tau _{2}^{2}(x-\mu )^{2}/2}{\bigr )},&x\geq \mu .\end{cases}}}$

That is, g(x) resembles a bell curve with its peak at x = μ, a spread/standard deviation of ${\displaystyle 1/\tau _{1}}$ to the left of the mean, and spread of ${\displaystyle 1/\tau _{2}}$ to the right of the mean. With the wavelength λ measured in nanometers, we then approximate the 1931 color matching functions:

${\displaystyle {\begin{aligned}{\overline {x}}(\lambda )&=1.056\,g(\lambda ;599.8,0.0264,0.0323)+0.362\,g(\lambda ;442.0,0.0624,0.0374)\\&\quad -0.065\,g(\lambda ;501.1,0.0490,0.0382),\\{\overline {y}}(\lambda )&=0.821\,g(\lambda ;568.8,0.0213,0.0247)+0.286\,g(\lambda ;530.9,0.0613,0.0322),\\{\overline {z}}(\lambda )&=1.217\,g(\lambda ;437.0,0.0845,0.0278)+0.681\,g(\lambda ;459.0,0.0385,0.0725).\end{aligned}}}$

The squared differences between the above approximation and the measured CIE xyz color matching functions is less than the within-observer variance encountered in the experimental measurements used to form the CIE standards. It is also possible to use fewer gaussian functions, with one gaussian for each "lobe". CIE 1964 fits well with a one-lobe function.^[15]

The CIE XYZ color matching functions are nonnegative, and lead to nonnegative XYZ coordinates for all real colors (that is, for nonnegative light spectra). Other observers, such as for the CIE RGB space or other RGB color spaces, are defined by other sets of three color-matching functions, not generally nonnegative, and lead to tristimulus values in those other spaces, which may include negative coordinates for some real colors.

Computing XYZ from spectral dataedit

Emissive caseedit

The tristimulus values for a color with a spectral radiance L_e,Ω,λ are given in terms of the standard observer by:

Zdroj:https://en.wikipedia.org?pojem=CIE_1931_color_space
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---