In physics and geometry, a catenary (US: /ˈkætənɛri/ KAT-ən-err-ee, UK: /kəˈtiːnəri/ kə-TEE-nər-ee) is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field.

The catenary curve has a U-like shape, superficially similar in appearance to a parabola, which it is not.

The curve appears in the design of certain types of arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings.

The catenary is also called the alysoid, chainette,^[1] or, particularly in the materials sciences, an example of a funicular.^[2] Rope statics describes catenaries in a classic statics problem involving a hanging rope.^[3]

Mathematically, the catenary curve is the graph of the hyperbolic cosine function. The surface of revolution of the catenary curve, the catenoid, is a minimal surface, specifically a minimal surface of revolution. A hanging chain will assume a shape of least potential energy which is a catenary.^[4] Galileo Galilei in 1638 discussed the catenary in the book Two New Sciences recognizing that it was different from a parabola. The mathematical properties of the catenary curve were studied by Robert Hooke in the 1670s, and its equation was derived by Leibniz, Huygens and Johann Bernoulli in 1691.

Catenaries and related curves are used in architecture and engineering (e.g., in the design of bridges and arches so that forces do not result in bending moments). In the offshore oil and gas industry, "catenary" refers to a steel catenary riser, a pipeline suspended between a production platform and the seabed that adopts an approximate catenary shape. In the rail industry it refers to the overhead wiring that transfers power to trains. (This often supports a contact wire, in which case it does not follow a true catenary curve.)

In optics and electromagnetics, the hyperbolic cosine and sine functions are basic solutions to Maxwell's equations.^[5] The symmetric modes consisting of two evanescent waves would form a catenary shape.^[6][7][8]

History

The word "catenary" is derived from the Latin word catēna, which means "chain". The English word "catenary" is usually attributed to Thomas Jefferson,^[9][10] who wrote in a letter to Thomas Paine on the construction of an arch for a bridge:

I have lately received from Italy a treatise on the equilibrium of arches, by the Abbé Mascheroni. It appears to be a very scientifical work. I have not yet had time to engage in it; but I find that the conclusions of his demonstrations are, that every part of the catenary is in perfect equilibrium.^[11]

It is often said^[12] that Galileo thought the curve of a hanging chain was parabolic. However, in his Two New Sciences (1638), Galileo wrote that a hanging cord is only an approximate parabola, correctly observing that this approximation improves in accuracy as the curvature gets smaller and is almost exact when the elevation is less than 45°.^[13] The fact that the curve followed by a chain is not a parabola was proven by Joachim Jungius (1587–1657); this result was published posthumously in 1669.^[12]

The application of the catenary to the construction of arches is attributed to Robert Hooke, whose "true mathematical and mechanical form" in the context of the rebuilding of St Paul's Cathedral alluded to a catenary.^[14] Some much older arches approximate catenaries, an example of which is the Arch of Taq-i Kisra in Ctesiphon.^[15]

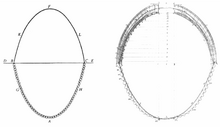
In 1671, Hooke announced to the Royal Society that he had solved the problem of the optimal shape of an arch, and in 1675 published an encrypted solution as a Latin anagram^[16] in an appendix to his Description of Helioscopes,^[17] where he wrote that he had found "a true mathematical and mechanical form of all manner of Arches for Building." He did not publish the solution to this anagram^[18] in his lifetime, but in 1705 his executor provided it as ut pendet continuum flexile, sic stabit contiguum rigidum inversum, meaning "As hangs a flexible cable so, inverted, stand the touching pieces of an arch."

In 1691, Gottfried Leibniz, Christiaan Huygens, and Johann Bernoulli derived the equation in response to a challenge by Jakob Bernoulli;^[12] their solutions were published in the Acta Eruditorum for June 1691.^[19][20] David Gregory wrote a treatise on the catenary in 1697^[12][21] in which he provided an incorrect derivation of the correct differential equation.^[20]

Euler proved in 1744 that the catenary is the curve which, when rotated about the x-axis, gives the surface of minimum surface area (the catenoid) for the given bounding circles.^[1] Nicolas Fuss gave equations describing the equilibrium of a chain under any force in 1796.^[22]

Inverted catenary arch

Catenary arches are often used in the construction of kilns. To create the desired curve, the shape of a hanging chain of the desired dimensions is transferred to a form which is then used as a guide for the placement of bricks or other building material.^[23][24]

The Gateway Arch in St. Louis, Missouri, United States is sometimes said to be an (inverted) catenary, but this is incorrect.^[25] It is close to a more general curve called a flattened catenary, with equation y = A cosh(Bx), which is a catenary if AB = 1. While a catenary is the ideal shape for a freestanding arch of constant thickness, the Gateway Arch is narrower near the top. According to the U.S. National Historic Landmark nomination for the arch, it is a "weighted catenary" instead. Its shape corresponds to the shape that a weighted chain, having lighter links in the middle, would form.^[26][27]

• 
  Catenary^[28] arches under the roof of Gaudí's Casa Milà, Barcelona, Spain.
• 
  The Sheffield Winter Garden is enclosed by a series of catenary arches.^[29]
• 
  The Gateway Arch (St. Louis, Missouri) is a flattened catenary.
• 
  Catenary arch kiln under construction over temporary form

Catenary bridges

In free-hanging chains, the force exerted is uniform with respect to length of the chain, and so the chain follows the catenary curve.^[30] The same is true of a simple suspension bridge or "catenary bridge," where the roadway follows the cable.^[31][32]

A stressed ribbon bridge is a more sophisticated structure with the same catenary shape.^[33][34]

However, in a suspension bridge with a suspended roadway, the chains or cables support the weight of the bridge, and so do not hang freely. In most cases the roadway is flat, so when the weight of the cable is negligible compared with the weight being supported, the force exerted is uniform with respect to horizontal distance, and the result is a parabola, as discussed below (although the term "catenary" is often still used, in an informal sense). If the cable is heavy then the resulting curve is between a catenary and a parabola.^[35][36]

Anchoring of marine objects

The catenary produced by gravity provides an advantage to heavy anchor rodes. An anchor rode (or anchor line) usually consists of chain or cable or both. Anchor rodes are used by ships, oil rigs, docks, floating wind turbines, and other marine equipment which must be anchored to the seabed.

When the rope is slack, the catenary curve presents a lower angle of pull on the anchor or mooring device than would be the case if it were nearly straight. This enhances the performance of the anchor and raises the level of force it will resist before dragging. To maintain the catenary shape in the presence of wind, a heavy chain is needed, so that only larger ships in deeper water can rely on this effect. Smaller boats also rely on catenary to maintain maximum holding power.^[37]

Cable ferries and chain boats present a special case of marine vehicles moving although moored by the two catenaries each of one or more cables (wire ropes or chains) passing through the vehicle and moved along by motorized sheaves. The catenaries can be evaluated graphically.^[38]

Mathematical description

Equation

The equation of a catenary in Cartesian coordinates has the form^[35]

where cosh is the hyperbolic cosine function, and where a is the distance of the lowest point above the x axis.^[39] All catenary curves are similar to each other, since changing the parameter a is equivalent to a uniform scaling of the curve.

The Whewell equation for the catenary is^[35]

where ${\displaystyle \varphi }$ is the tangential angle and s the arc length.

Differentiating gives

and eliminating ${\displaystyle \varphi }$ gives the Cesàro equation^[40] where ${\displaystyle \kappa }$ is the curvature.

The radius of curvature is then

which is the length of the normal between the curve and the x-axis.^[41]

Relation to other curves

When a parabola is rolled along a straight line, the roulette curve traced by its focus is a catenary.^[42] The envelope of the directrix of the parabola is also a catenary.^[43] The involute from the vertex, that is the roulette traced by a point starting at the vertex when a line is rolled on a catenary, is the tractrix.^[42]

Another roulette, formed by rolling a line on a catenary, is another line. This implies that square wheels can roll perfectly smoothly on a road made of a series of bumps in the shape of an inverted catenary curve. The wheels can be any regular polygon except a triangle, but the catenary must have parameters corresponding to the shape and dimensions of the wheels.^[44]

Geometrical properties

Over any horizontal interval, the ratio of the area under the catenary to its length equals a, independent of the interval selected. The catenary is the only plane curve other than a horizontal line with this property. Also, the geometric centroid of the area under a stretch of catenary is the midpoint of the perpendicular segment connecting the centroid of the curve itself and the x-axis.^[45]

Science

A moving charge in a uniform electric field travels along a catenary (which tends to a parabola if the charge velocity is much less than the speed of light c).^[46]

The surface of revolution with fixed radii at either end that has minimum surface area is a catenary revolved about the x-axis.^[42]

Analysis

Model of chains and arches

In the mathematical model the chain (or cord, cable, rope, string, etc.) is idealized by assuming that it is so thin that it can be regarded as a curve and that it is so flexible any force of tension exerted by the chain is parallel to the chain.^[47] The analysis of the curve for an optimal arch is similar except that the forces of tension become forces of compression and everything is inverted.^[48] An underlying principle is that the chain may be considered a rigid body once it has attained equilibrium.^[49] Equations which define the shape of the curve and the tension of the chain at each point may be derived by a careful inspection of the various forces acting on a segment using the fact that these forces must be in balance if the chain is in static equilibrium.

Let the path followed by the chain be given parametrically by r = (x, y) = (x(s), y(s)) where s represents arc length and r is the position vector. This is the natural parameterization and has the property that

where u is a unit tangent vector.

A differential equation for the curve may be derived as follows.^[50] Let c be the lowest point on the chain, called the vertex of the catenary.^[51] The slope dy/dx of the curve is zero at c since it is a minimum point. Assume r is to the right of c since the other case is implied by symmetry. The forces acting on the section of the chain from c to r are the tension of the chain at c, the tension of the chain at r, and the weight of the chain. The tension at c is tangent to the curve at c and is therefore horizontal without any vertical component and it pulls the section to the left so it may be written (−T₀, 0) where T₀ is the magnitude of the force. The tension at r is parallel to the curve at r and pulls the section to the right. The tension at r can be split into two components so it may be written Tu = (T cos φ, T sin φ), where T is the magnitude of the force and φ is the angle between the curve at r and the x-axis (see tangential angle). Finally, the weight of the chain is represented by (0, −ws) where w is the weight per unit length and s is the length of the segment of chain between c and r.

The chain is in equilibrium so the sum of three forces is 0, therefore

and

and dividing these gives

It is convenient to write

which is the length of chain whose weight is equal in magnitude to the tension at c.^[52] Then