Chaos theory is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities.^[1] Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization.^[2] The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions).^[3] A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.^[4][5][6]

Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general.^[7] This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution^[8] and is fully determined by their initial conditions, with no random elements involved.^[9] In other words, the deterministic nature of these systems does not make them predictable.^[10][11] This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:^[12]

Chaos: When the present determines the future but the approximate present does not approximately determine the future.

Chaotic behavior exists in many natural systems, including fluid flow, heartbeat irregularities, weather and climate.^[13][14][8] It also occurs spontaneously in some systems with artificial components, such as road traffic.^[2] This behavior can be studied through the analysis of a chaotic mathematical model or through analytical techniques such as recurrence plots and Poincaré maps. Chaos theory has applications in a variety of disciplines, including meteorology,^[8] anthropology,^[15] sociology, environmental science, computer science, engineering, economics, ecology, and pandemic crisis management.^[16][17] The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory and self-assembly processes.

Introduction

Chaos theory concerns deterministic systems whose behavior can, in principle, be predicted. Chaotic systems are predictable for a while and then 'appear' to become random. The amount of time for which the behavior of a chaotic system can be effectively predicted depends on three things: how much uncertainty can be tolerated in the forecast, how accurately its current state can be measured, and a time scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, about 1 millisecond; weather systems, a few days (unproven); the inner solar system, 4 to 5 million years.^[18] In chaotic systems, the uncertainty in a forecast increases exponentially with elapsed time. Hence, mathematically, doubling the forecast time more than squares the proportional uncertainty in the forecast. This means, in practice, a meaningful prediction cannot be made over an interval of more than two or three times the Lyapunov time. When meaningful predictions cannot be made, the system appears random.^[19]

Chaos theory is a method of qualitative and quantitative analysis to investigate the behavior of dynamic systems that cannot be explained and predicted by single data relationships, but must be explained and predicted by whole, continuous data relationships.

Chaotic dynamics

In common usage, "chaos" means "a state of disorder".^[20][21] However, in chaos theory, the term is defined more precisely. Although no universally accepted mathematical definition of chaos exists, a commonly used definition, originally formulated by Robert L. Devaney, says that to classify a dynamical system as chaotic, it must have these properties:^[22]

1. it must be sensitive to initial conditions,
2. it must be topologically transitive,
3. it must have dense periodic orbits.

In some cases, the last two properties above have been shown to actually imply sensitivity to initial conditions.^[23][24] In the discrete-time case, this is true for all continuous maps on metric spaces.^[25] In these cases, while it is often the most practically significant property, "sensitivity to initial conditions" need not be stated in the definition.

If attention is restricted to intervals, the second property implies the other two.^[26] An alternative and a generally weaker definition of chaos uses only the first two properties in the above list.^[27]

Sensitivity to initial conditions

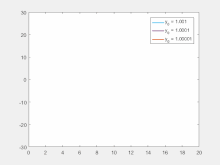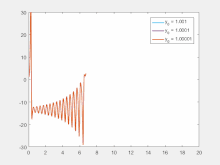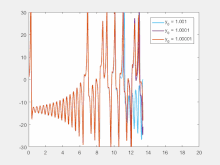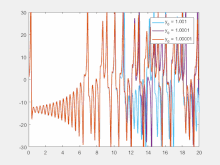
Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.^[2]

Sensitivity to initial conditions is popularly known as the "butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C., entitled Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?.^[28] The flapping wing represents a small change in the initial condition of the system, which causes a chain of events that prevents the predictability of large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the overall system could have been vastly different.

As suggested in Lorenz's book entitled The Essence of Chaos, published in 1993,^[5] "sensitive dependence can serve as an acceptable definition of chaos". In the same book, Lorenz defined the butterfly effect as: "The phenomenon that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration." The above definition is consistent with the sensitive dependence of solutions on initial conditions (SDIC). An idealized skiing model was developed to illustrate the sensitivity of time-varying paths to initial positions.^[5] A predictability horizon can be determined before the onset of SDIC (i.e., prior to significant separations of initial nearby trajectories).^[29]

A consequence of sensitivity to initial conditions is that if we start with a limited amount of information about the system (as is usually the case in practice), then beyond a certain time, the system would no longer be predictable. This is most prevalent in the case of weather, which is generally predictable only about a week ahead.^[30] This does not mean that one cannot assert anything about events far in the future—only that some restrictions on the system are present. For example, we know that the temperature of the surface of the earth will not naturally reach 100 °C (212 °F) or fall below −130 °C (−202 °F) on earth (during the current geologic era), but we cannot predict exactly which day will have the hottest temperature of the year.

In more mathematical terms, the Lyapunov exponent measures the sensitivity to initial conditions, in the form of rate of exponential divergence from the perturbed initial conditions.^[31] More specifically, given two starting trajectories in the phase space that are infinitesimally close, with initial separation ${\displaystyle \delta \mathbf {Z} _{0}}$, the two trajectories end up diverging at a rate given by

${\displaystyle |\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|,}$

where ${\displaystyle t}$ is the time and ${\displaystyle \lambda }$ is the Lyapunov exponent. The rate of separation depends on the orientation of the initial separation vector, so a whole spectrum of Lyapunov exponents can exist. The number of Lyapunov exponents is equal to the number of dimensions of the phase space, though it is common to just refer to the largest one. For example, the maximal Lyapunov exponent (MLE) is most often used, because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.^[8]

In addition to the above property, other properties related to sensitivity of initial conditions also exist. These include, for example, measure-theoretical mixing (as discussed in ergodic theory) and properties of a K-system.^[11]

Non-periodicity

A chaotic system may have sequences of values for the evolving variable that exactly repeat themselves, giving periodic behavior starting from any point in that sequence. However, such periodic sequences are repelling rather than attracting, meaning that if the evolving variable is outside the sequence, however close, it will not enter the sequence and in fact, will diverge from it. Thus for almost all initial conditions, the variable evolves chaotically with non-periodic behavior.

Topological mixing

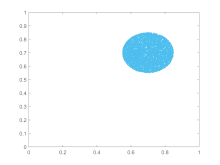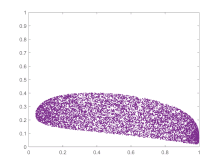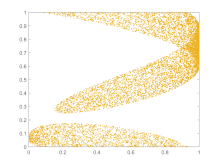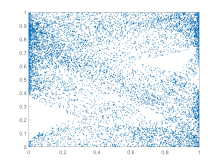
Topological mixing (or the weaker condition of topological transitivity) means that the system evolves over time so that any given region or open set of its phase space eventually overlaps with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.

Topological mixing is often omitted from popular accounts of chaos, which equate chaos with only sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points eventually becomes widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behavior: all points except 0 tend to positive or negative infinity.

Topological transitivity

A map ${\displaystyle f:X\to X}$ is said to be topologically transitive if for any pair of non-empty open sets ${\displaystyle U,V\subset X}$, there exists ${\displaystyle k>0}$ such that ${\displaystyle f^{k}(U)\cap V\neq \emptyset }$. Topological transitivity is a weaker version of topological mixing. Intuitively, if a map is topologically transitive then given a point x and a region V, there exists a point y near x whose orbit passes through V. This implies that it is impossible to decompose the system into two open sets.^[32]

An important related theorem is the Birkhoff Transitivity Theorem. It is easy to see that the existence of a dense orbit implies topological transitivity. The Birkhoff Transitivity Theorem states that if X is a second countable, complete metric space, then topological transitivity implies the existence of a dense set of points in X that have dense orbits.^[33]

Density of periodic orbits

For a chaotic system to have dense periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits.^[32] The one-dimensional logistic map defined by x → 4 x (1 – x) is one of the simplest systems with density of periodic orbits. For example, ${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$ → ${\displaystyle {\tfrac {5+{\sqrt {5}}}{8}}}$ → ${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$ (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).^[34]

Sharkovskii's theorem is the basis of the Li and Yorke^[35] (1975) proof that any continuous one-dimensional system that exhibits a regular cycle of period three will also display regular cycles of every other length, as well as completely chaotic orbits.

Strange attractors

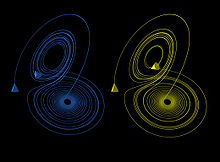
Some dynamical systems, like the one-dimensional logistic map defined by x → 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor, since then a large set of initial conditions leads to orbits that converge to this chaotic region.^[36]

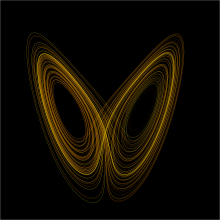
An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it is not only one of the first, but it is also one of the most complex, and as such gives rise to a very interesting pattern that, with a little imagination, looks like the wings of a butterfly.

Unlike fixed-point attractors and limit cycles, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set, which forms at the boundary between basins of attraction of fixed points. Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and the fractal dimension can be calculated for them.

Coexisting attractors

In contrast to single type chaotic solutions, recent studies using Lorenz models ^[40][41] have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models,^[37][38][39] suggested a revised view that "the entirety of weather possesses a dual nature of chaos and order with distinct predictability", in contrast to the conventional view of "weather is chaotic".

Minimum complexity of a chaotic system

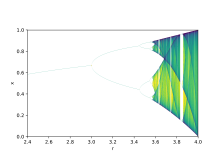
Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. In contrast, for continuous dynamical systems, the Poincaré–Bendixson theorem shows that a strange attractor can only arise in three or more dimensions. Finite-dimensional linear systems are never chaotic; for a dynamical system to display chaotic behavior, it must be either nonlinear or infinite-dimensional.

The Poincaré–Bendixson theorem states that a two-dimensional differential equation has very regular behavior. The Lorenz attractor discussed below is generated by a system of three differential equations such as:

Zdroj:https://en.wikipedia.org?pojem=Chaos_Theory
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---