Geodesy
Fundamentals Geodesy Geodynamics Geomatics History
Concepts Geographical distance Geoid Figure of the Earth (radius and circumference) Geodetic coordinates Geodetic datum Geodesic Horizontal position representation Latitude / Longitude Map projection Reference ellipsoid Satellite geodesy Spatial reference system Spatial relations Vertical positions
Technologies Global Nav. Sat. Systems (GNSSs) Global Pos. System (GPS) GLONASS (Russia) BeiDou (BDS) (China) Galileo (Europe) NAVIC (India) Quasi-Zenith Sat. Sys. (QZSS) (Japan) Discrete Global Grid and Geocoding
Standards (history) NGVD 29 Sea Level Datum 1929 OSGB36 Ordnance Survey Great Britain 1936 SK-42 Systema Koordinat 1942 goda ED50 European Datum 1950 SAD69 South American Datum 1969 GRS 80 Geodetic Reference System 1980 ISO 6709 Geographic point coord. 1983 NAD 83 North American Datum 1983 WGS 84 World Geodetic System 1984 NAVD 88 N. American Vertical Datum 1988 ETRS89 European Terrestrial Ref. Sys. 1989 GCJ-02 Chinese obfuscated datum 2002 Geo URI Internet link to a point 2010 International Terrestrial Reference System Spatial Reference System Identifier (SRID) Universal Transverse Mercator (UTM)
v t e

The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry (Euler 1755).

If the Earth is treated as a sphere, the geodesics are great circles (all of which are closed) and the problems reduce to ones in spherical trigonometry. However, Newton (1687) showed that the effect of the rotation of the Earth results in its resembling a slightly oblate ellipsoid: in this case, the equator and the meridians are the only simple closed geodesics. Furthermore, the shortest path between two points on the equator does not necessarily run along the equator. Finally, if the ellipsoid is further perturbed to become a triaxial ellipsoid (with three distinct semi-axes), only three geodesics are closed.

Geodesics on an ellipsoid of revolution

There are several ways of defining geodesics (Hilbert & Cohn-Vossen 1952, pp. 220–221). A simple definition is as the shortest path between two points on a surface. However, it is frequently more useful to define them as paths with zero geodesic curvature—i.e., the analogue of straight lines on a curved surface. This definition encompasses geodesics traveling so far across the ellipsoid's surface that they start to return toward the starting point, so that other routes are more direct, and includes paths that intersect or re-trace themselves. Short enough segments of a geodesics are still the shortest route between their endpoints, but geodesics are not necessarily globally minimal (i.e. shortest among all possible paths). Every globally-shortest path is a geodesic, but not vice versa.

By the end of the 18th century, an ellipsoid of revolution (the term spheroid is also used) was a well-accepted approximation to the figure of the Earth. The adjustment of triangulation networks entailed reducing all the measurements to a reference ellipsoid and solving the resulting two-dimensional problem as an exercise in spheroidal trigonometry (Bomford 1952, Chap. 3) (Leick et al. 2015, §4.5).

It is possible to reduce the various geodesic problems into one of two types. Consider two points: A at latitude φ₁ and longitude λ₁ and B at latitude φ₂ and longitude λ₂ (see Fig. 1). The connecting geodesic (from A to B) is AB, of length s₁₂, which has azimuths α₁ and α₂ at the two endpoints.^[1] The two geodesic problems usually considered are:

1. the direct geodesic problem or first geodesic problem, given A, α₁, and s₁₂, determine B and α₂;
2. the inverse geodesic problem or second geodesic problem, given A and B, determine s₁₂, α₁, and α₂.

As can be seen from Fig. 1, these problems involve solving the triangle NAB given one angle, α₁ for the direct problem and λ₁₂ = λ₂ − λ₁ for the inverse problem, and its two adjacent sides. For a sphere the solutions to these problems are simple exercises in spherical trigonometry, whose solution is given by formulas for solving a spherical triangle. (See the article on great-circle navigation.)

For an ellipsoid of revolution, the characteristic constant defining the geodesic was found by Clairaut (1735). A systematic solution for the paths of geodesics was given by Legendre (1806) and Oriani (1806) (and subsequent papers in 1808 and 1810). The full solution for the direct problem (complete with computational tables and a worked out example) is given by Bessel (1825).

During the 18th century geodesics were typically referred to as "shortest lines". The term "geodesic line" (actually, a curve) was coined by Laplace (1799b):

Nous désignerons cette ligne sous le nom de ligne géodésique .

This terminology was introduced into English either as "geodesic line" or as "geodetic line", for example (Hutton 1811, p. 115),

A line traced in the manner we have now been describing, or deduced from trigonometrical measures, by the means we have indicated, is called a geodetic or geodesic line: it has the property of being the shortest which can be drawn between its two extremities on the surface of the Earth; and it is therefore the proper itinerary measure of the distance between those two points.

In its adoption by other fields geodesic line, frequently shortened to geodesic, was preferred.

This section treats the problem on an ellipsoid of revolution (both oblate and prolate). The problem on a triaxial ellipsoid is covered in the next section.

Equations for a geodesic

Fig. 2. Differential element of a meridian ellipse.

Fig. 3. Differential element of a geodesic on an ellipsoid.

Here the equations for a geodesic are developed; the derivation closely follows that of Bessel (1825). Jordan & Eggert (1941), Bagratuni (1962, §15), Gan'shin (1967, Chap. 5), Krakiwsky & Thomson (1974, §4), Rapp (1993, §1.2), Jekeli (2012), and Borre & Strang (2012) also provide derivations of these equations.

Consider an ellipsoid of revolution with equatorial radius a and polar semi-axis b. Define the flattening f, the eccentricity e, and the second eccentricity e′:

${\displaystyle f={\frac {a-b}{a}},\quad e={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\sqrt {f(2-f)}},\quad e'={\frac {\sqrt {a^{2}-b^{2}}}{b}}={\frac {e}{1-f}}.}$

(In most applications in geodesy, the ellipsoid is taken to be oblate, a > b; however, the theory applies without change to prolate ellipsoids, a < b, in which case f, e², and e′² are negative.)

Let an elementary segment of a path on the ellipsoid have length ds. From Figs. 2 and 3, we see that if its azimuth is α, then ds is related to dφ and dλ by

${\displaystyle \cos \alpha \,ds=\rho \,d\varphi =-{\frac {dR}{\sin \varphi }},\quad \sin \alpha \,ds=R\,d\lambda ,}$ (1)

where ρ is the meridional radius of curvature, R = ν cosφ is the radius of the circle of latitude φ, and ν is the normal radius of curvature. The elementary segment is therefore given by

${\displaystyle ds^{2}=\rho ^{2}\,d\varphi ^{2}+R^{2}\,d\lambda ^{2}}$

or

${\displaystyle {\begin{aligned}ds&={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\&\equiv L(\varphi ,\varphi ')\,d\lambda ,\end{aligned}}}$

where φ′ = dφ/dλ and the Lagrangian function L depends on φ through ρ(φ) and R(φ). The length of an arbitrary path between (φ₁, λ₁) and (φ₂, λ₂) is given by

${\displaystyle s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi ,\varphi ')\,d\lambda ,}$

where φ is a function of λ satisfying φ(λ₁) = φ₁ and φ(λ₂) = φ₂. The shortest path or geodesic entails finding that function φ(λ) which minimizes s₁₂. This is an exercise in the calculus of variations and the minimizing condition is given by the Beltrami identity,

${\displaystyle L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}}$

Substituting for L and using Eqs. (1) gives

${\displaystyle R\sin \alpha ={\text{const.}}}$

Clairaut (1735) found this relation, using a geometrical construction; a similar derivation is presented by Lyusternik (1964, §10).^[2] Differentiating this relation gives

${\displaystyle d\alpha =\sin \varphi \,d\lambda .}$

This, together with Eqs. (1), leads to a system of ordinary differential equations for a geodesic

${\displaystyle {\frac {d\varphi }{ds}}={\frac {\cos \alpha }{\rho }};\quad {\frac {d\lambda }{ds}}={\frac {\sin \alpha }{\nu \cos \varphi }};\quad {\frac {d\alpha }{ds}}={\frac {\tan \varphi \sin \alpha }{\nu }}.}$

We can express R in terms of the parametric latitude, β, using

${\displaystyle R=a\cos \beta ,}$

and Clairaut's relation then becomes

${\displaystyle \sin \alpha _{1}\cos \beta _{1}=\sin \alpha _{2}\cos \beta _{2}.}$

Fig. 4. Geodesic problem mapped to the auxiliary sphere.

Fig. 5. The elementary geodesic problem on the auxiliary sphere.

This is the sine rule of spherical trigonometry relating two sides of the triangle NAB (see Fig. 4), NA = 1⁄2π − β₁, and NB = 1⁄2π − β₂ and their opposite angles B = π − α₂ and A = α₁.

In order to find the relation for the third side AB = σ₁₂, the spherical arc length, and included angle N = ω₁₂, the spherical longitude, it is useful to consider the triangle NEP representing a geodesic starting at the equator; see Fig. 5. In this figure, the variables referred to the auxiliary sphere are shown with the corresponding quantities for the ellipsoid shown in parentheses. Quantities without subscripts refer to the arbitrary point P; E, the point at which the geodesic crosses the equator in the northward direction, is used as the origin for σ, s and ω.

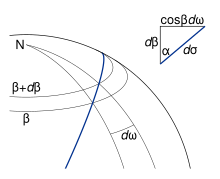
If the side EP is extended by moving P infinitesimally (see Fig. 6), we obtain

${\displaystyle \cos <!--\; \; -->\mathrm{\alpha <!--\; \alpha \; -->}d\mathrm{\sigma <!--\; \sigma \; -->}=d\mathrm{\beta <!--\; \beta \; -->},\sin <!--\; \; -->\mathrm{\alpha <!--\; \alpha \; -->}d\mathrm{\sigma <!--\; \sigma \; -->}=\cos <!--\; \; -->\mathrm{\beta <!--\; \beta \; -->}d}$Zdroj:https://en.wikipedia.org?pojem=Earth_geodesic
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---