It has been suggested that Ekman spiral be merged into this article. (Discuss) Proposed since March 2024.

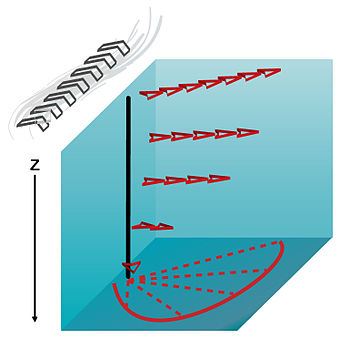
The Ekman layer is the layer in a fluid where there is a force balance between pressure gradient force, Coriolis force and turbulent drag. It was first described by Vagn Walfrid Ekman. Ekman layers occur both in the atmosphere and in the ocean.

There are two types of Ekman layers. The first type occurs at the surface of the ocean and is forced by surface winds, which act as a drag on the surface of the ocean. The second type occurs at the bottom of the atmosphere and ocean, where frictional forces are associated with flow over rough surfaces.

History

Ekman developed the theory of the Ekman layer after Fridtjof Nansen observed that ice drifts at an angle of 20°–40° to the right of the prevailing wind direction while on an Arctic expedition aboard the Fram. Nansen asked his colleague, Vilhelm Bjerknes to set one of his students upon study of the problem. Bjerknes tapped Ekman, who presented his results in 1902 as his doctoral thesis.^[1]

Mathematical formulation

The mathematical formulation of the Ekman layer begins by assuming a neutrally stratified fluid, a balance between the forces of pressure gradient, Coriolis and turbulent drag.

${\displaystyle {\begin{aligned}-fv&=-{\frac {1}{\rho _{o}}}{\frac {\partial p}{\partial x}}+K_{m}{\frac {\partial ^{2}u}{\partial z^{2}}},\\fu&=-{\frac {1}{\rho _{o}}}{\frac {\partial p}{\partial y}}+K_{m}{\frac {\partial ^{2}v}{\partial z^{2}}},\\0&=-{\frac {1}{\rho _{o}}}{\frac {\partial p}{\partial z}},\end{aligned}}}$

where ${\displaystyle \ u}$ and ${\displaystyle \ v}$ are the velocities in the ${\displaystyle \ x}$ and ${\displaystyle \ y}$ directions, respectively, ${\displaystyle \ f}$ is the local Coriolis parameter, and ${\displaystyle \ K_{m}}$ is the diffusive eddy viscosity, which can be derived using mixing length theory. Note that ${\displaystyle p}$ is a modified pressure: we have incorporated the hydrostatic of the pressure, to take account of gravity.

There are many regions where an Ekman layer is theoretically plausible; they include the bottom of the atmosphere, near the surface of the earth and ocean, the bottom of the ocean, near the sea floor and at the top of the ocean, near the air-water interface. Different boundary conditions are appropriate for each of these different situations. Each of these situations can be accounted for through the boundary conditions applied to the resulting system of ordinary differential equations. The separate cases of top and bottom boundary layers are shown below.

Ekman layer at the ocean (or free) surface

We will consider boundary conditions of the Ekman layer in the upper ocean:^[2]

${\displaystyle {\text{at }}z=0:\quad A{\frac {\partial u}{\partial z}}=\tau ^{x}\quad {\text{and}}\quad A{\frac {\partial v}{\partial z}}=\tau ^{y},}$

where ${\displaystyle \ \tau ^{x}}$ and ${\displaystyle \ \tau ^{y}}$ are the components of the surface stress, ${\displaystyle \ \tau }$, of the wind field or ice layer at the top of the ocean, and ${\displaystyle \ A\equiv \rho K_{m}}$ is the dynamic viscosity.

For the boundary condition on the other side, as ${\displaystyle \ z\to -\infty :u\to u_{g},v\to v_{g}}$, where ${\displaystyle \ u_{g}}$ and ${\displaystyle \ v_{g}}$ are the geostrophic flows in the ${\displaystyle \ x}$ and ${\displaystyle \ y}$ directions.

Solution

These differential equations can be solved to find:

Zdroj:https://en.wikipedia.org?pojem=Ekman_layer
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---