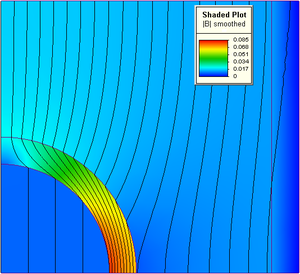
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.

The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain.^[1] The simple equations that model these finite elements are then assembled into a larger system of equations that models the entire problem. The FEM then approximates a solution by minimizing an associated error function via the calculus of variations.

Studying or analyzing a phenomenon with FEM is often referred to as finite element analysis (FEA).

Basic concepts

FEM mesh created by an analyst before finding a solution to a magnetic problem using FEM software. Colors indicate that the analyst has set material properties for each zone, in this case, a conducting wire coil in orange; a ferromagnetic component (perhaps iron) in light blue; and air in grey. Although the geometry may seem simple, it would be very challenging to calculate the magnetic field for this setup without FEM software using equations alone.

FEM solution to the problem at left, involving a cylindrically shaped magnetic shield. The ferromagnetic cylindrical part shields the area inside the cylinder by diverting the magnetic field created by the coil (rectangular area on the right). The color represents the amplitude of the magnetic flux density, as indicated by the scale in the inset legend, red being high amplitude. The area inside the cylinder is low amplitude (dark blue, with widely spaced lines of magnetic flux), which suggests that the shield is performing as it was designed to.

The subdivision of a whole domain into simpler parts has several advantages:^[2]

• Accurate representation of complex geometry
• Inclusion of dissimilar material properties
• Easy representation of the total solution
• Capture of local effects.

Typical work out of the method involves:

1. dividing the domain of the problem into a collection of subdomains, with each subdomain represented by a set of element equations to the original problem
2. systematically recombining all sets of element equations into a global system of equations for the final calculation.

The global system of equations has known solution techniques and can be calculated from the initial values of the original problem to obtain a numerical answer.

In the first step above, the element equations are simple equations that locally approximate the original complex equations to be studied, where the original equations are often partial differential equations (PDE). To explain the approximation in this process, the finite element method is commonly introduced as a special case of Galerkin method. The process, in mathematical language, is to construct an integral of the inner product of the residual and the weight functions and set the integral to zero. In simple terms, it is a procedure that minimizes the approximation error by fitting trial functions into the PDE. The residual is the error caused by the trial functions, and the weight functions are polynomial approximation functions that project the residual. The process eliminates all the spatial derivatives from the PDE, thus approximating the PDE locally with

• a set of algebraic equations for steady state problems,
• a set of ordinary differential equations for transient problems.

These equation sets are element equations. They are linear if the underlying PDE is linear and vice versa. Algebraic equation sets that arise in the steady-state problems are solved using numerical linear algebra methods. In contrast, ordinary differential equation sets that occur in the transient problems are solved by numerical integration using standard techniques such as Euler's method or the Runge-Kutta method.

In step (2) above, a global system of equations is generated from the element equations by transforming coordinates from the subdomains' local nodes to the domain's global nodes. This spatial transformation includes appropriate orientation adjustments as applied in relation to the reference coordinate system. The process is often carried out by FEM software using coordinate data generated from the subdomains.

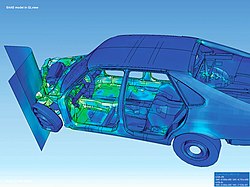
The practical application of FEM is known as finite element analysis (FEA). FEA as applied in engineering, is a computational tool for performing engineering analysis. It includes the use of mesh generation techniques for dividing a complex problem into small elements, as well as the use of software coded with a FEM algorithm. In applying FEA, the complex problem is usually a physical system with the underlying physics such as the Euler–Bernoulli beam equation, the heat equation, or the Navier-Stokes equations expressed in either PDE or integral equations, while the divided small elements of the complex problem represent different areas in the physical system.

FEA may be used for analyzing problems over complicated domains (like cars and oil pipelines) when the domain changes (as during a solid-state reaction with a moving boundary), when the desired precision varies over the entire domain, or when the solution lacks smoothness. FEA simulations provide a valuable resource as they remove multiple instances of creating and testing complex prototypes for various high-fidelity situations.^{[citation needed]} For example, in a frontal crash simulation, it is possible to increase prediction accuracy in "important" areas like the front of the car and reduce it in its rear (thus reducing the cost of the simulation). Another example would be in numerical weather prediction, where it is more important to have accurate predictions over developing highly nonlinear phenomena (such as tropical cyclones in the atmosphere, or eddies in the ocean) rather than relatively calm areas.

A clear, detailed, and practical presentation of this approach can be found in The Finite Element Method for Engineers.^[3]

History

While it is difficult to quote the date of the invention of the finite element method, the method originated from the need to solve complex elasticity and structural analysis problems in civil and aeronautical engineering.^[4] Its development can be traced back to work by Alexander Hrennikoff^[5] and Richard Courant^[6] in the early 1940s. Another pioneer was Ioannis Argyris. In the USSR, the introduction of the practical application of the method is usually connected with the name of Leonard Oganesyan.^[7] It was also independently rediscovered in China by Feng Kang in the later 1950s and early 1960s, based on the computations of dam constructions, where it was called the finite difference method based on variation principle. Although the approaches used by these pioneers are different, they share one essential characteristic: mesh discretization of a continuous domain into a set of discrete sub-domains, usually called elements.

Hrennikoff's work discretizes the domain by using a lattice analogy, while Courant's approach divides the domain into finite triangular subregions to solve second order elliptic partial differential equations that arise from the problem of torsion of a cylinder. Courant's contribution was evolutionary, drawing on a large body of earlier results for PDEs developed by Lord Rayleigh, Walther Ritz, and Boris Galerkin.

The finite element method obtained its real impetus in the 1960s and 1970s by the developments of J. H. Argyris with co-workers at the University of Stuttgart, R. W. Clough with co-workers at UC Berkeley, O. C. Zienkiewicz with co-workers Ernest Hinton, Bruce Irons^[8] and others at Swansea University, Philippe G. Ciarlet at the University of Paris 6 and Richard Gallagher with co-workers at Cornell University. Further impetus was provided in these years by available open-source finite element programs. NASA sponsored the original version of NASTRAN. UC Berkeley made the finite element programs SAP IV^[9] and later OpenSees widely available. In Norway, the ship classification society Det Norske Veritas (now DNV GL) developed Sesam in 1969 for use in the analysis of ships.^[10] A rigorous mathematical basis to the finite element method was provided in 1973 with the publication by Gilbert Strang and George Fix.^[11] The method has since been generalized for the numerical modeling of physical systems in a wide variety of engineering disciplines, e.g., electromagnetism, heat transfer, and fluid dynamics.^[12][13]

Technical discussion

The structure of finite element methods

A finite element method is characterized by a variational formulation, a discretization strategy, one or more solution algorithms, and post-processing procedures.

Examples of the variational formulation are the Galerkin method, the discontinuous Galerkin method, mixed methods, etc.

A discretization strategy is understood to mean a clearly defined set of procedures that cover (a) the creation of finite element meshes, (b) the definition of basis function on reference elements (also called shape functions), and (c) the mapping of reference elements onto the elements of the mesh. Examples of discretization strategies are the h-version, p-version, hp-version, x-FEM, isogeometric analysis, etc. Each discretization strategy has certain advantages and disadvantages. A reasonable criterion in selecting a discretization strategy is to realize nearly optimal performance for the broadest set of mathematical models in a particular model class.

Various numerical solution algorithms can be classified into two broad categories; direct and iterative solvers. These algorithms are designed to exploit the sparsity of matrices that depend on the variational formulation and discretization strategy choices.

Post-processing procedures are designed to extract the data of interest from a finite element solution. To meet the requirements of solution verification, postprocessors need to provide for a posteriori error estimation in terms of the quantities of interest. When the errors of approximation are larger than what is considered acceptable, then the discretization has to be changed either by an automated adaptive process or by the action of the analyst. Some very efficient postprocessors provide for the realization of superconvergence.

Illustrative problems P1 and P2

The following two problems demonstrate the finite element method.

P1 is a one-dimensional problem

$${\displaystyle {\text{ P1 }}:{\begin{cases}u''(x)=f(x){\text{ in }}(0,1),\\u(0)=u(1)=0,\end{cases}}}$$

${\displaystyle f}$

${\displaystyle u}$

${\displaystyle x}$

${\displaystyle u''}$

${\displaystyle u}$

${\displaystyle x}$

P2 is a two-dimensional problem (Dirichlet problem)