Group velocity

Frequency dispersion in groups of gravity waves on the surface of deep water. The red square moves with the phase velocity, and the green circles propagate with the group velocity. In this deep-water case, *the phase velocity is twice the group velocity*. The red square overtakes two green circles when moving from the left to the right of the figure.
New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.
For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases.

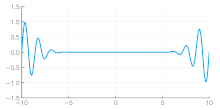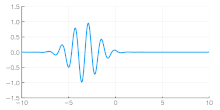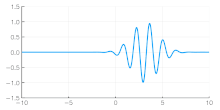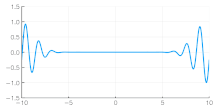
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the modulation or envelope of the wave—propagates through space.

For example, if a stone is thrown into the middle of a very still pond, a circular pattern of waves with a quiescent center appears in the water, also known as a capillary wave. The expanding ring of waves is the wave group or wave packet, within which one can discern individual waves that travel faster than the group as a whole. The amplitudes of the individual waves grow as they emerge from the trailing edge of the group and diminish as they approach the leading edge of the group.

History

The idea of a group velocity distinct from a wave's phase velocity was first proposed by W.R. Hamilton in 1839, and the first full treatment was by Rayleigh in his "Theory of Sound" in 1877.^[2]

Definition and interpretation

The group velocity $v g$ is defined by the equation:^[3]^[4]^[5]^[6]

v_{\rm {g}}\ \equiv \ {\frac {\partial \omega }{\partial k}}\,

where $ω$ is the wave's angular frequency (usually expressed in radians per second), and $k$ is the angular wavenumber (usually expressed in radians per meter). The phase velocity is: $v p = ω / k$ .

The function $ω (k)$ , which gives $ω$ as a function of $k$ , is known as the dispersion relation.

If $ω$ is directly proportional to $k$ , then the group velocity is exactly equal to the phase velocity. A wave of any shape will travel undistorted at this velocity.
If ω is a linear function of k, but not directly proportional $(ω = ak + b)$ , then the group velocity and phase velocity are different. The envelope of a wave packet (see figure on right) will travel at the group velocity, while the individual peaks and troughs within the envelope will move at the phase velocity.
If $ω$ is not a linear function of $k$ , the envelope of a wave packet will become distorted as it travels. Since a wave packet contains a range of different frequencies (and hence different values of $k$ ), the group velocity $\partialω/\partialk$ will be different for different values of $k$ . Therefore, the envelope does not move at a single velocity, but its wavenumber components ( $k$ ) move at different velocities, distorting the envelope. If the wavepacket has a narrow range of frequencies, and $ω (k)$ is approximately linear over that narrow range, the pulse distortion will be small, in relation to the small nonlinearity. See further discussion below. For example, for deep water gravity waves, ${\textstyle \omega ={\sqrt {gk}}}$ , and hence $v g = v p /2$ .
This underlies the Kelvin wake pattern for the bow wave of all ships and swimming objects. Regardless of how fast they are moving, as long as their velocity is constant, on each side the wake forms an angle of 19.47° = arcsin(1/3) with the line of travel.^[7]

Derivation

One derivation of the formula for group velocity is as follows.^[8]^[9]

Consider a wave packet as a function of position $x$ and time $t : α (x, t)$ .

Let $A (k)$ be its Fourier transform at time $t = 0$ ,

\alpha (x,0)=\int _{-\infty }^{\infty }dk\,A(k)e^{ikx}.

By the superposition principle, the wavepacket at any time $t$ is

\alpha (x,t)=\int _{-\infty }^{\infty }dk\,A(k)e^{i(kx-\omega t)},

where $ω$ is implicitly a function of $k$ .

Assume that the wave packet $α$ is almost monochromatic, so that $A (k)$ is sharply peaked around a central wavenumber $k 0$ .

Then, linearization gives

\omega (k)\approx \omega _{0}+\left(k-k_{0}\right)\omega '_{0}

where

\omega _{0}=\omega (k_{0})

and

\omega '_{0}=\left.{\frac {\partial \omega (k)}{\partial k}}\right|_{k=k_{0}}

(see next section for discussion of this step). Then, after some algebra,

\alpha (x,t)=e^{i\left(k_{0}x-\omega _{0}t\right)}\int _{-\infty }^{\infty }dk\,A(k)e^{i(k-k_{0})\left(x-\omega '_{0}t\right)}.

There are two factors in this expression. The first factor, $e^{i\left(k_{0}x-\omega _{0}t\right)}$ , describes a perfect monochromatic wave with wavevector $k 0$ , with peaks and troughs moving at the phase velocity $\omega _{0}/k_{0}$ within the envelope of the wavepacket.