This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This scientific article needs additional citations to secondary or tertiary sources. Help add sources such as review articles, monographs, or textbooks. Please also establish the relevance for any primary research articles cited. Unsourced or poorly sourced material may be challenged and removed. (July 2023) (Learn how and when to remove this message) The article's lead section may need to be rewritten. Relevant discussion may be found on Talk:Hill sphere. Please help improve the lead and read the lead layout guide. (April 2024) (Learn how and when to remove this message) (Learn how and when to remove this message)

Part of a series on
Astrodynamics
Orbital mechanics
Orbital elements Apsis Argument of periapsis Eccentricity Inclination Mean anomaly Orbital nodes Semi-major axis True anomaly
Types of two-body orbits by eccentricity Circular orbit Elliptic orbit Transfer orbit (Hohmann transfer orbit Bi-elliptic transfer orbit) Parabolic orbit Hyperbolic orbit Radial orbit Decaying orbit
Equations Dynamical friction Escape velocity Kepler's equation Kepler's laws of planetary motion Orbital period Orbital velocity Surface gravity Specific orbital energy Vis-viva equation
Celestial mechanics
Gravitational influences Barycenter Hill sphere Perturbations Sphere of influence
N-body orbits Lagrangian points (Halo orbits) Lissajous orbits Lyapunov orbits
Engineering and efficiency
Preflight engineering Mass ratio Payload fraction Propellant mass fraction Tsiolkovsky rocket equation
Efficiency measures Gravity assist Oberth effect
Propulsive maneuvers Orbital maneuver Orbit insertion
v t e

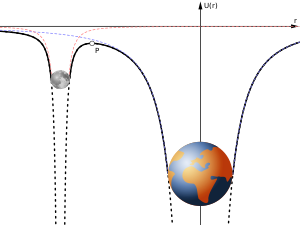
The Hill sphere is a common model for the calculation of a gravitational sphere of influence. It is the most commonly used model to calculate the spatial extent of gravitational influence of an astronomical body (m) in which it dominates over the gravitational influence of other bodies, particularly a primary (M).^[1] It is sometimes confused with other models of gravitational influence, such as the Laplace sphere^[1] or being called the Roche sphere, the latter causing confusion with the Roche limit.^[2][3] It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.^{[not verified in body]}

To be retained by a more gravitationally attracting astrophysical object—a planet by a more massive star, a moon by a more massive planet—the less massive body must have an orbit that lies within the gravitational potential represented by the more massive body's Hill sphere.^{[not verified in body]} That moon would, in turn, have a Hill sphere of its own, and any object within that distance would tend to become a satellite of the moon, rather than of the planet itself.^{[not verified in body]}

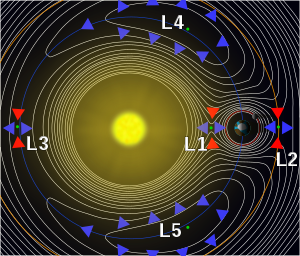
One simple view of the extent of the Solar System is that it is bounded by the Hill sphere of the Sun (engendered by the Sun's interaction with the galactic nucleus or other more massive stars).^{[4][verification needed]} A more complex example is the one at right, the Earth's Hill sphere, which extends between the Lagrange points L₁ and L₂,^{[clarification needed]} which lie along the line of centers of the Earth and the more massive Sun.^{[not verified in body]} The gravitational influence of the less massive body is least in that direction, and so it acts as the limiting factor for the size of the Hill sphere;^{[clarification needed]} beyond that distance, a third object in orbit around the Earth would spend at least part of its orbit outside the Hill sphere, and would be progressively perturbed by the tidal forces of the more massive body, the Sun, eventually ending up orbiting the latter.^{[not verified in body]}

For two massive bodies with gravitational potentials and any given energy of a third object of negligible mass interacting with them, one can define a zero-velocity surface in space which cannot be passed, the contour of the Jacobi integral.^{[not verified in body]} When the object's energy is low, the zero-velocity surface completely surrounds the less massive body (of this restricted three-body system), which means the third object cannot escape; at higher energy, there will be one or more gaps or bottlenecks by which the third object may escape the less massive body and go into orbit around the more massive one.^{[not verified in body]} If the energy is at the border between these two cases, then the third object cannot escape, but the zero-velocity surface confining it touches a larger zero-velocity surface around the less massive body^{[verification needed]} at one of the nearby Lagrange points, forming a cone-like point there.^{[clarification needed][not verified in body]} At the opposite side of the less massive body, the zero-velocity surface gets close to the other Lagrange point.^{[not verified in body]} This limiting zero-velocity surface around the less massive body is its Hill "sphere".^{[according to whom?][original research?]}

Definition

This section needs expansion with: a comprehensive definition of the title subject, drawn from multiple secondary and tertiary sources, that can be summarised in the lead. You can help by adding to it. (July 2023)

The Hill radius or sphere (the latter defined by the former radius^{[citation needed]}) has been described as "the region around a planetary body where its own gravity (compared to that of the Sun or other nearby bodies) is the dominant force in attracting satellites," both natural and artificial.^{[5][better source needed]}

As described by de Pater and Lissauer, all bodies within a system such as the Sun's Solar System "feel the gravitational force of one another", and while the motions of just two gravitationally interacting bodies—constituting a "two-body problem"—are "completely integrable (...there exists one independent integral or constraint per degree of freedom)" and thus an exact, analytic solution, the interactions of three (or more) such bodies "cannot be deduced analytically", requiring instead solutions by numerical integration, when possible.^[6]: p.26 This is the case, unless the negligible mass of one of the three bodies allows approximation of the system as a two-body problem, known formally as a "restricted three-body problem".^[6]: p.26

For such two- or restricted three-body problems as its simplest examples—e.g., one more massive primary astrophysical body, mass of m1, and a less massive secondary body, mass of m2—the concept of a Hill radius or sphere is of the approximate limit to the secondary mass's "gravitational dominance",^[6] a limit defined by "the extent" of its Hill sphere, which is represented mathematically as follows:^{[6]: p.29 [7]}

${\displaystyle R_{\mathrm {H} }\approx a{\sqrt{\frac {m_{2}}{3(m_{1}+m_{2})}}}}$,

where, in this representation, major axis "a" can be understood as the "instantaneous heliocentric distance" between the two masses (elsewhere abbreviated rp).^{[6]: p.29 [7]}

More generally, if the less massive body, ${\displaystyle m2}$, orbits a more massive body (m1, e.g., as a planet orbiting around the Sun) and has a semi-major axis ${\displaystyle a}$, and an eccentricity of ${\displaystyle e}$, then the Hill radius or sphere, ${\displaystyle R_{\mathrm {H} }}$ of the less massive body, calculated at the pericenter, is approximately:^{[8][non-primary source needed][better source needed]}

${\displaystyle R_{\mathrm {H} }\approx a(1-e){\sqrt{\frac {m_{2}}{3(m_{1}+m_{2})}}}.}$

When eccentricity is negligible (the most favourable case for orbital stability), this expression reduces to the one presented above.^{[citation needed]}

Example and derivation

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. Find sources: "Hill sphere" – news · newspapers · books · scholar · JSTOR (December 2023) (Learn how and when to remove this message)

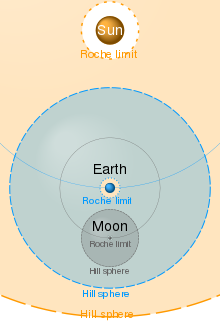
In the Earth-Sun example, the Earth (5.97×10²⁴ kg) orbits the Sun (1.99×10³⁰ kg) at a distance of 149.6 million km, or one astronomical unit (AU). The Hill sphere for Earth thus extends out to about 1.5 million km (0.01 AU). The Moon's orbit, at a distance of 0.384 million km from Earth, is comfortably within the gravitational sphere of influence of Earth and it is therefore not at risk of being pulled into an independent orbit around the Sun.

The earlier eccentricity-ignoring formula can be re-stated as follows:

${\displaystyle {\frac {R_{\mathrm {H} }^{3}}{a^{3}}}\approx 1/3{\frac {m2}{M}}}$, or ${\displaystyle 3{\frac {R_{\mathrm {H} }^{3}}{a^{3}}}\approx {\frac {m2}{M}}}$,

where M is the sum of the interacting masses.

Derivation

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2023) (Learn how and when to remove this message)

The expression for the Hill radius can be found by equating gravitational and centrifugal forces acting on a test particle (of mass much smaller than ${\displaystyle m}$) orbiting the secondary body. Assume that the distance between masses ${\displaystyle M}$ and ${\displaystyle m}$ is ${\displaystyle r}$, and that the test particle is orbiting at a distance ${\displaystyle r_{\mathrm {H} }}$ from the secondary. When the test particle is on the line connecting the primary and the secondary body, the force balance requires that

${\displaystyle {\frac {Gm}{r_{\mathrm {H} }^{2}}}-{\frac {GM}{(r-r_{\mathrm {H} })^{2}}}+\Omega ^{2}(r-r_{\mathrm {H} })=0,}$

where ${\displaystyle G}$ is the gravitational constant and ${\displaystyle \Omega ={\sqrt {\frac {GM}{r^{3}}}}}$ is the (Keplerian) angular velocity of the secondary about the primary (assuming that ${\displaystyle m\ll M}$). The above equation can also be written as

${\displaystyle {\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)^{-2}+{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)=0,}$

which, through a binomial expansion to leading order in ${\displaystyle r_{\mathrm {H} }/r}$, can be written as

${\displaystyle \frac{m}{r_{\mathrm{H}}^2}-<!--\; -\; -->\frac{M}{r^2}\left(1+2\frac{r_{\mathrm{H}}}{r}\right)+\frac{M}{r^2}\left(1-<!--\; -\; -->\frac{r_{\mathrm{H}}}{r}\right)=\frac{m}{}}$Zdroj:https://en.wikipedia.org?pojem=Hill_radius
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---