A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (elements), usually arranged along a common axis. Lenses are made from materials such as glass or plastic and are ground, polished, or molded to the required shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called "lenses", such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses.

Lenses are used in various imaging devices such as telescopes, binoculars, and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia.

History

This section needs expansion with: history after 1758. You can help by adding to it. (January 2012)

The word lens comes from lēns, the Latin name of the lentil (a seed of a lentil plant), because a double-convex lens is lentil-shaped. The lentil also gives its name to a geometric figure.^[a]

Some scholars argue that the archeological evidence indicates that there was widespread use of lenses in antiquity, spanning several millennia.^[1] The so-called Nimrud lens is a rock crystal artifact dated to the 7th century BCE which may or may not have been used as a magnifying glass, or a burning glass.^[2][3][4] Others have suggested that certain Egyptian hieroglyphs depict "simple glass meniscal lenses".^{[5][verification needed]}

The oldest certain reference to the use of lenses is from Aristophanes' play The Clouds (424 BCE) mentioning a burning-glass.^[6] Pliny the Elder (1st century) confirms that burning-glasses were known in the Roman period.^[7] Pliny also has the earliest known reference to the use of a corrective lens when he mentions that Nero was said to watch the gladiatorial games using an emerald (presumably concave to correct for nearsightedness, though the reference is vague).^[8] Both Pliny and Seneca the Younger (3 BC–65 AD) described the magnifying effect of a glass globe filled with water.

Ptolemy (2nd century) wrote a book on Optics, which however survives only in the Latin translation of an incomplete and very poor Arabic translation. The book was, however, received by medieval scholars in the Islamic world, and commented upon by Ibn Sahl (10th century), who was in turn improved upon by Alhazen (Book of Optics, 11th century). The Arabic translation of Ptolemy's Optics became available in Latin translation in the 12th century (Eugenius of Palermo 1154). Between the 11th and 13th century "reading stones" were invented. These were primitive plano-convex lenses initially made by cutting a glass sphere in half. The medieval (11th or 12th century) rock crystal Visby lenses may or may not have been intended for use as burning glasses.^[9]

Spectacles were invented as an improvement of the "reading stones" of the high medieval period in Northern Italy in the second half of the 13th century.^[10] This was the start of the optical industry of grinding and polishing lenses for spectacles, first in Venice and Florence in the late 13th century,^[11] and later in the spectacle-making centres in both the Netherlands and Germany.^[12] Spectacle makers created improved types of lenses for the correction of vision based more on empirical knowledge gained from observing the effects of the lenses (probably without the knowledge of the rudimentary optical theory of the day).^[13][14] The practical development and experimentation with lenses led to the invention of the compound optical microscope around 1595, and the refracting telescope in 1608, both of which appeared in the spectacle-making centres in the Netherlands.^[15][16]

With the invention of the telescope and microscope there was a great deal of experimentation with lens shapes in the 17th and early 18th centuries by those trying to correct chromatic errors seen in lenses. Opticians tried to construct lenses of varying forms of curvature, wrongly assuming errors arose from defects in the spherical figure of their surfaces.^[17] Optical theory on refraction and experimentation was showing no single-element lens could bring all colours to a focus. This led to the invention of the compound achromatic lens by Chester Moore Hall in England in 1733, an invention also claimed by fellow Englishman John Dollond in a 1758 patent.

Construction of simple lenses

Most lenses are spherical lenses: their two surfaces are parts of the surfaces of spheres. Each surface can be convex (bulging outwards from the lens), concave (depressed into the lens), or planar (flat). The line joining the centres of the spheres making up the lens surfaces is called the axis of the lens. Typically the lens axis passes through the physical centre of the lens, because of the way they are manufactured. Lenses may be cut or ground after manufacturing to give them a different shape or size. The lens axis may then not pass through the physical centre of the lens.

Toric or sphero-cylindrical lenses have surfaces with two different radii of curvature in two orthogonal planes. They have a different focal power in different meridians. This forms an astigmatic lens. An example is eyeglass lenses that are used to correct astigmatism in someone's eye.

Types of simple lenses

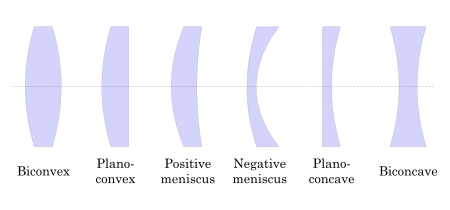
Lenses are classified by the curvature of the two optical surfaces. A lens is biconvex (or double convex, or just convex) if both surfaces are convex. If both surfaces have the same radius of curvature, the lens is equiconvex. A lens with two concave surfaces is biconcave (or just concave). If one of the surfaces is flat, the lens is plano-convex or plano-concave depending on the curvature of the other surface. A lens with one convex and one concave side is convex-concave or meniscus. Convex-concave lenses are most commonly used in corrective lenses, since the shape minimizes some aberrations.

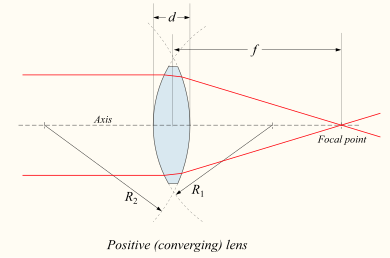
If the lens is biconvex or plano-convex, a collimated beam of light passing through the lens converges to a spot (a focus) behind the lens. In this case, the lens is called a positive or converging lens. For a thin lens in air, the distance from the lens to the spot is the focal length of the lens, which is commonly represented by f in diagrams and equations. An extended hemispherical lens is a special type of plano-convex lens, in which the lens's curved surface is a full hemisphere and the lens is much thicker than the radius of curvature.

Another extreme case of a thick convex lens is a ball lens, whose shape is completely round. When used in novelty photography it is often called a "lensball". A ball-shaped lens has the advantage of being omnidirectional, but for most optical glass types, its focal point lies close to the ball's surface . Because of the ball's curvature extremes compared to the lens size, optical aberration is much worse than thin lenses, with the notable exception of chromatic aberration.

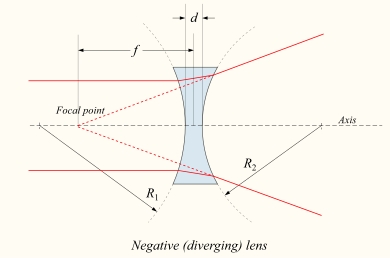
If the lens is biconcave or plano-concave, a collimated beam of light passing through the lens is diverged (spread); the lens is thus called a negative or diverging lens. The beam, after passing through the lens, appears to emanate from a particular point on the axis in front of the lens. For a thin lens in air, the distance from this point to the lens is the focal length, though it is negative with respect to the focal length of a converging lens.

Convex-concave (meniscus) lenses can be either positive or negative, depending on the relative curvatures of the two surfaces. A negative meniscus lens has a steeper concave surface (with a shorter radius than the convex surface) and is thinner at the centre than at the periphery. Conversely, a positive meniscus lens has a steeper convex surface (with a shorter radius than the concave surface) and is thicker at the centre than at the periphery.

An ideal thin lens with two surfaces of equal curvature would have zero optical power, meaning that it would neither converge nor diverge light. All real lenses have a nonzero thickness, however, which makes a real lens with identical curved surfaces slightly positive. To obtain exactly zero optical power, a meniscus lens must have slightly unequal curvatures to account for the effect of the lens' thickness.

For a spherical surface

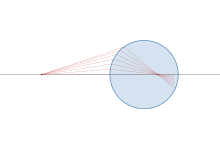
For a single refraction for a circular boundary, the relation between object and image is given by^[18][19]

$${\displaystyle {\frac {n_{2}}{v}}+{\frac {n_{1}}{u}}={\frac {n_{2}-n_{1}}{R}}}$$

where R is the radius of the spherical surface, n₂ is the refractive index of the surface, and n₁ is the refractive index of medium.

Applying this on the two spherical surfaces of a thin lens leads to the lens maker's formula.

Derivation

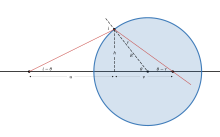
Applying Snell's law on the spherical surface, ${\displaystyle n_{1}\sin i=n_{2}\sin r\,.}$

Also in the diagram,

$${\displaystyle {\begin{aligned}\tan(i-\theta )&={\frac {h}{u}}\\\tan(\theta -r)&={\frac {h}{v}}\\\sin \theta &={\frac {h}{R}}\end{aligned}}}$$

Using small angle approximation and eliminating i, r, and θ,

$${\displaystyle {\frac {n_{2}}{v}}+{\frac {n_{1}}{u}}={\frac {n_{2}-n_{1}}{R}}\,.}$$

Lensmaker's equation

The focal length of a lens in air can be calculated from the lensmaker's equation:^[20]

$${\displaystyle {\frac {1}{\ f\ }}=(n-1)\left\ ,}$$

• f  is the (effective) focal length of the lens;
• n is the refractive index of the lens material;
• R₁ is the (signed, see below) radius of curvature of the lens surface closer to the light source;
• R₂ is the radius of curvature of the lens surface farther from the light source; and
• d is the thickness of the lens (the distance along the lens axis between the two surface vertices).

The focal length f is with respect to the principal planes of the lens, and the locations of the planes ${\textstyle h_{1}}$ and ${\textstyle h_{2}}$ with respect to the respective lens vertices are given by the following formulas, where it is a positive value if it is right to the respective vertex.^[21]

$${\displaystyle h_{1}=-{\frac {f(n-1)d}{R_{2}n}}}$$

$${\displaystyle h_{2}=-{\frac {f(n-1)d}{R_{1}n}}}$$

f is positive for converging lenses, and negative for diverging lenses. The reciprocal of the focal length, f⁻¹, is the optical power of the lens. If the focal length is in metres, this gives the optical power in dioptres (inverse metres).

Lenses have the same focal length when light travels from the back to the front as when light goes from the front to the back. Other properties of the lens, such as the aberrations are not the same in both directions.

Sign convention for radii of curvature R₁ and R₂

The signs of the lens' radii of curvature indicate whether the corresponding surfaces are convex or concave. The sign convention used to represent this varies^{[citation needed]}, but in this article a positive R indicates a surface's center of curvature is further along in the direction of the ray travel (right, in the accompanying diagrams), while negative R means that rays reaching the surface have already passed the center of curvature. Consequently, for external lens surfaces as diagrammed above, R₁ > 0 and R₂ < 0 indicate convex surfaces (used to converge light in a positive lens), while R₁ < 0 and R₂ > 0 indicate concave surfaces. The reciprocal of the radius of curvature is called the curvature. A flat surface has zero curvature, and its radius of curvature is infinite.

Thin lens approximation

If d is small compared to R₁ and R₂ then the thin lens approximation can be made. For a lens in air, f  is then given by^[22]