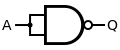A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

A logic gate is a device that performs a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one that has, for instance, zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device[1] (see ideal and real op-amps for comparison).
The primary way of building logic gates uses diodes or transistors acting as electronic switches. Today, most logic gates are made from MOSFETs (metal–oxide–semiconductor field-effect transistors).[2] They can also be constructed using vacuum tubes, electromagnetic relays with relay logic, fluidic logic, pneumatic logic, optics, molecules, acoustics,[3] or even mechanical or thermal[4] elements.
Logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of Boolean logic, and therefore, all of the algorithms and mathematics that can be described with Boolean logic. Logic circuits include such devices as multiplexers, registers, arithmetic logic units (ALUs), and computer memory, all the way up through complete microprocessors,[5] which may contain more than 100 million logic gates.
Compound logic gates AND-OR-Invert (AOI) and OR-AND-Invert (OAI) are often employed in circuit design because their construction using MOSFETs is simpler and more efficient than the sum of the individual gates.[6]
History and development
The binary number system was refined by Gottfried Wilhelm Leibniz (published in 1705), influenced by the ancient I Ching's binary system.[7][8] Leibniz established that using the binary system combined the principles of arithmetic and logic.
In an 1886 letter, Charles Sanders Peirce described how logical operations could be carried out by electrical switching circuits.[9] Early electro-mechanical computers were constructed from switches and relay logic rather than the later innovations of vacuum tubes (thermionic valves) or transistors (from which later electronic computers were constructed). Ludwig Wittgenstein introduced a version of the 16-row truth table as proposition 5.101 of Tractatus Logico-Philosophicus (1921). Walther Bothe, inventor of the coincidence circuit, got part of the 1954 Nobel Prize in physics, for the first modern electronic AND gate in 1924. Konrad Zuse designed and built electromechanical logic gates for his computer Z1 (from 1935 to 1938).
From 1934 to 1936, NEC engineer Akira Nakashima, Claude Shannon and Victor Shestakov introduced switching circuit theory in a series of papers showing that two-valued Boolean algebra, which they discovered independently, can describe the operation of switching circuits.[10][11][12][13] Using this property of electrical switches to implement logic is the fundamental concept that underlies all electronic digital computers. Switching circuit theory became the foundation of digital circuit design, as it became widely known in the electrical engineering community during and after World War II, with theoretical rigor superseding the ad hoc methods that had prevailed previously.[13]
Metal–oxide–semiconductor (MOS) devices in the forms of PMOS and NMOS were demonstrated by Bell Labs engineers Mohamed M. Atalla and Dawon Kahng in 1960.[14] Both types were later combined and adapted into complementary MOS (CMOS) logic by Chih-Tang Sah and Frank Wanlass at Fairchild Semiconductor in 1963.[15]
Symbols

There are two sets of symbols for elementary logic gates in common use, both defined in ANSI/IEEE Std 91-1984 and its supplement ANSI/IEEE Std 91a-1991. The "distinctive shape" set, based on traditional schematics, is used for simple drawings and derives from United States Military Standard MIL-STD-806 of the 1950s and 1960s.[16] It is sometimes unofficially described as "military", reflecting its origin. The "rectangular shape" set, based on ANSI Y32.14 and other early industry standards as later refined by IEEE and IEC, has rectangular outlines for all types of gate and allows representation of a much wider range of devices than is possible with the traditional symbols.[17] The IEC standard, IEC 60617-12, has been adopted by other standards, such as EN 60617-12:1999 in Europe, BS EN 60617-12:1999 in the United Kingdom, and DIN EN 60617-12:1998 in Germany.
The mutual goal of IEEE Std 91-1984 and IEC 617-12 was to provide a uniform method of describing the complex logic functions of digital circuits with schematic symbols. These functions were more complex than simple AND and OR gates. They could be medium-scale circuits such as a 4-bit counter to a large-scale circuit such as a microprocessor.
IEC 617-12 and its renumbered successor IEC 60617-12 do not explicitly show the "distinctive shape" symbols, but do not prohibit them.[17] These are, however, shown in ANSI/IEEE Std 91 (and 91a) with this note: "The distinctive-shape symbol is, according to IEC Publication 617, Part 12, not preferred, but is not considered to be in contradiction to that standard." IEC 60617-12 correspondingly contains the note (Section 2.1) "Although non-preferred, the use of other symbols recognized by official national standards, that is distinctive shapes in place of symbols , shall not be considered to be in contradiction with this standard. Usage of these other symbols in combination to form complex symbols (for example, use as embedded symbols) is discouraged." This compromise was reached between the respective IEEE and IEC working groups to permit the IEEE and IEC standards to be in mutual compliance with one another.
In the 1980s, schematics were the predominant method to design both circuit boards and custom ICs known as gate arrays. Today custom ICs and the field-programmable gate array are typically designed with Hardware Description Languages (HDL) such as Verilog or VHDL.
| Type | Distinctive shape (IEEE Std 91/91a-1991) |
Rectangular shape (IEEE Std 91/91a-1991) (IEC 60617-12:1997) |
Boolean algebra between A and B | Truth table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Single-input gates | ||||||||||||||||||||||
| Buffer |
| |||||||||||||||||||||
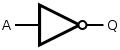
| NOT (inverter) |
or |
| ||||||||||||||||||||
| In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble and is used in logic diagrams to indicate a logic negation between the external logic state and the internal logic state (1 to 0 or vice versa). On a circuit diagram it must be accompanied by a statement asserting that the positive logic convention or negative logic convention is being used (high voltage level = 1 or low voltage level = 1, respectively). The wedge is used in circuit diagrams to directly indicate an active-low (low voltage level = 1) input or output without requiring a uniform convention throughout the circuit diagram. This is called Direct Polarity Indication. See IEEE Std 91/91A and IEC 60617-12. Both the bubble and the wedge can be used on distinctive-shape and rectangular-shape symbols on circuit diagrams, depending on the logic convention used. On pure logic diagrams, only the bubble is meaningful. | ||||||||||||||||||||||
| Conjunction and disjunction | ||||||||||||||||||||||
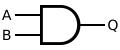
| AND | or |
| ||||||||||||||||||||
| OR | or |
| ||||||||||||||||||||
| Alternative denial and joint denial | ||||||||||||||||||||||
| NAND | or |
| ||||||||||||||||||||
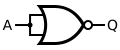
| NOR | 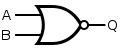
|

|
or |
| ||||||||||||||||||
| Exclusive or and biconditional | ||||||||||||||||||||||
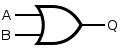
| XOR | 
|

|
or |
| ||||||||||||||||||
| The output of a two input exclusive-OR is true only when the two input values are different, and false if they are equal, regardless of the value. If there are more than two inputs, the output of the distinctive-shape symbol is undefined. The output of the rectangular-shaped symbol is true if the number of true inputs is exactly one or exactly the number following the "=" in the qualifying symbol. | ||||||||||||||||||||||
| XNOR | 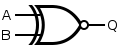
|
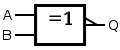
|
or |
| ||||||||||||||||||
De Morgan equivalent symbols
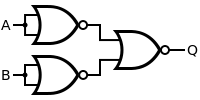
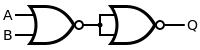
By use of De Morgan's laws, an AND function is identical to an OR function with negated inputs and outputs. Likewise, an OR function is identical to an AND function with negated inputs and outputs. A NAND gate is equivalent to an OR gate with negated inputs, and a NOR gate is equivalent to an AND gate with negated inputs.
This leads to an alternative set of symbols for basic gates that use the opposite core symbol (AND or OR) but with the inputs and outputs negated. Use of these alternative symbols can make logic circuit diagrams much clearer and help to show accidental connection of an active high output to an active low input or vice versa. Any connection that has logic negations at both ends can be replaced by a negationless connection and a suitable change of gate or vice versa. Any connection that has a negation at one end and no negation at the other can be made easier to interpret by instead using the De Morgan equivalent symbol at either of the two ends. When negation or polarity indicators on both ends of a connection match, there is no logic negation in that path (effectively, bubbles "cancel"), making it easier to follow logic states from one symbol to the next. This is commonly seen in real logic diagrams – thus the reader must not get into the habit of associating the shapes exclusively as OR or AND shapes, but also take into account the bubbles at both inputs and outputs in order to determine the "true" logic function indicated.
A De Morgan symbol can show more clearly a gate's primary logical purpose and the polarity of its nodes that are considered in the "signaled" (active, on) state. Consider the simplified case where a two-input NAND gate is used to drive a motor when either of its inputs are brought low by a switch. The "signaled" state (motor on) occurs when either one OR the other switch is on. Unlike a regular NAND symbol, which suggests AND logic, the De Morgan version, a two negative-input OR gate, correctly shows that OR is of interest. The regular NAND symbol has a bubble at the output and none at the inputs (the opposite of the states that will turn the motor on), but the De Morgan symbol shows both inputs and output in the polarity that will drive the motor.
De Morgan's theorem is most commonly used to implement logic gates as combinations of only NAND gates, or as combinations of only NOR gates, for economic reasons.
Truth tables
Output comparison of various logic gates:
| Input | Output | |
| A | Buffer | Inverter |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| Input | Output | ||||||
| A | B | AND | NAND | OR | NOR | XOR | XNOR |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Universal logic gates
Charles Sanders Peirce (during 1880–1881) showed that NOR gates alone (or alternatively NAND gates alone) can be used to reproduce the functions of all the other logic gates, but his work on it was unpublished until 1933.[18] The first published proof was by Henry M. Sheffer in 1913, so the NAND logical operation is sometimes called Sheffer stroke; the logical NOR is sometimes called Peirce's arrow.[19] Consequently, these gates are sometimes called universal logic gates.[20]