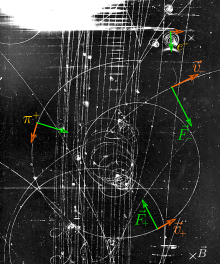
In physics, specifically in electromagnetism, the Lorentz force (or electromagnetic force) is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force (in SI units^[1][2]) of $${\displaystyle \mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right).}$$ It says that the electromagnetic force on a charge q is a combination of (1) a force in the direction of the electric field E (proportional to the magnitude of the field and the quantity of charge), and (2) a force at right angles to both the magnetic field B and the velocity v of the charge (proportional to the magnitude of the field, the charge, and the velocity).

Variations on this basic formula describe the magnetic force on a current-carrying wire (sometimes called Laplace force), the electromotive force in a wire loop moving through a magnetic field (an aspect of Faraday's law of induction), and the force on a moving charged particle.^[3]

Historians suggest that the law is implicit in a paper by James Clerk Maxwell, published in 1865.^[4] Hendrik Lorentz arrived at a complete derivation in 1895,^[5] identifying the contribution of the electric force a few years after Oliver Heaviside correctly identified the contribution of the magnetic force.^[6]

Lorentz force law as the definition of E and B

Trajectory of a particle with a positive or negative charge q under the influence of a magnetic field B, which is directed perpendicularly out of the screen.

Beam of electrons moving in a circle, due to the presence of a magnetic field. Purple light revealing the electron's path in this Teltron tube is created by the electrons colliding with gas molecules.

Charged particles experiencing the Lorentz force.

In many textbook treatments of classical electromagnetism, the Lorentz force law is used as the definition of the electric and magnetic fields E and B.^[7][8][9] To be specific, the Lorentz force is understood to be the following empirical statement:

The electromagnetic force F on a test charge at a given point and time is a certain function of its charge q and velocity v, which can be parameterized by exactly two vectors E and B, in the functional form: $${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$$

This is valid, even for particles approaching the speed of light (that is, magnitude of v, |v| ≈ c).^[10] So the two vector fields E and B are thereby defined throughout space and time, and these are called the "electric field" and "magnetic field". The fields are defined everywhere in space and time with respect to what force a test charge would receive regardless of whether a charge is present to experience the force.

As a definition of E and B, the Lorentz force is only a definition in principle because a real particle (as opposed to the hypothetical "test charge" of infinitesimally-small mass and charge) would generate its own finite E and B fields, which would alter the electromagnetic force that it experiences.^[11] In addition, if the charge experiences acceleration, as if forced into a curved trajectory, it emits radiation that causes it to lose kinetic energy. See for example Bremsstrahlung and synchrotron light. These effects occur through both a direct effect (called the radiation reaction force) and indirectly (by affecting the motion of nearby charges and currents).

Equation

Charged particle

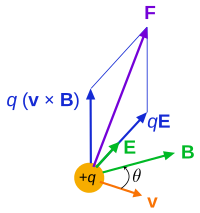
The force F acting on a particle of electric charge q with instantaneous velocity v, due to an external electric field E and magnetic field B, is given by (in SI units^[1]):^[12]

where × is the vector cross product (all boldface quantities are vectors). In terms of Cartesian components, we have: $${\displaystyle {\begin{aligned}F_{x}&=q\left(E_{x}+v_{y}B_{z}-v_{z}B_{y}\right),\\F_{y}&=q\left(E_{y}+v_{z}B_{x}-v_{x}B_{z}\right),\\F_{z}&=q\left(E_{z}+v_{x}B_{y}-v_{y}B_{x}\right).\end{aligned}}}$$

In general, the electric and magnetic fields are functions of the position and time. Therefore, explicitly, the Lorentz force can be written as: $${\displaystyle \mathbf {F} \left(\mathbf {r} (t),{\dot {\mathbf {r} }}(t),t,q\right)=q\left}$$ in which r is the position vector of the charged particle, t is time, and the overdot is a time derivative.

A positively charged particle will be accelerated in the same linear orientation as the E field, but will curve perpendicularly to both the instantaneous velocity vector v and the B field according to the right-hand rule (in detail, if the fingers of the right hand are extended to point in the direction of v and are then curled to point in the direction of B, then the extended thumb will point in the direction of F).

The term qE is called the electric force, while the term q(v × B) is called the magnetic force.^[13] According to some definitions, the term "Lorentz force" refers specifically to the formula for the magnetic force,^[14] with the total electromagnetic force (including the electric force) given some other (nonstandard) name. This article will not follow this nomenclature: In what follows, the term "Lorentz force" will refer to the expression for the total force.

The magnetic force component of the Lorentz force manifests itself as the force that acts on a current-carrying wire in a magnetic field. In that context, it is also called the Laplace force.

The Lorentz force is a force exerted by the electromagnetic field on the charged particle, that is, it is the rate at which linear momentum is transferred from the electromagnetic field to the particle. Associated with it is the power which is the rate at which energy is transferred from the electromagnetic field to the particle. That power is $${\displaystyle \mathbf {v} \cdot \mathbf {F} =q\,\mathbf {v} \cdot \mathbf {E} .}$$ Notice that the magnetic field does not contribute to the power because the magnetic force is always perpendicular to the velocity of the particle.

Continuous charge distribution

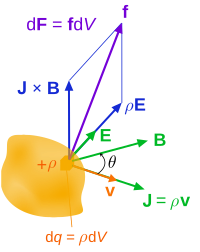
For a continuous charge distribution in motion, the Lorentz force equation becomes: $${\displaystyle \mathrm {d} \mathbf {F} =\mathrm {d} q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$$ where ${\displaystyle \mathrm {d} \mathbf {F} }$ is the force on a small piece of the charge distribution with charge ${\displaystyle \mathrm {d} q}$. If both sides of this equation are divided by the volume of this small piece of the charge distribution ${\displaystyle \mathrm {d} V}$, the result is: $${\displaystyle \mathbf {f} =\rho \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$$ where ${\displaystyle \mathbf {f} }$ is the force density (force per unit volume) and ${\displaystyle \rho }$ is the charge density (charge per unit volume). Next, the current density corresponding to the motion of the charge continuum is $${\displaystyle \mathbf {J} =\rho \mathbf {v} }$$Zdroj:https://en.wikipedia.org?pojem=Lorentz_force
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.