Modulo operator

In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the modulus of the operation).

Given two positive numbers $a$ and $n$ , $a$ modulo $n$ (often abbreviated as $a mod n$ ) is the remainder of the Euclidean division of $a$ by $n$ , where $a$ is the dividend and $n$ is the divisor.^[1]

For example, the expression "5 mod 2" evaluates to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1, while "9 mod 3" would evaluate to 0, because 9 divided by 3 has a quotient of 3 and a remainder of 0.

Although typically performed with $a$ and $n$ both being integers, many computing systems now allow other types of numeric operands. The range of values for an integer modulo operation of $n$ is 0 to $n - 1$ ( $a$ mod 1 is always 0; $a mod 0$ is undefined, being a division by zero).

When exactly one of $a$ or $n$ is negative, the basic definition breaks down, and programming languages differ in how these values are defined.

Variants of the definition

In mathematics, the result of the modulo operation is an equivalence class, and any member of the class may be chosen as representative; however, the usual representative is the least positive residue, the smallest non-negative integer that belongs to that class (i.e., the remainder of the Euclidean division).^[2] However, other conventions are possible. Computers and calculators have various ways of storing and representing numbers; thus their definition of the modulo operation depends on the programming language or the underlying hardware.

In nearly all computing systems, the quotient $q$ and the remainder $r$ of $a$ divided by $n$ satisfy the following conditions:

{\begin{aligned}&q\in \mathbb {Z} \\&a=nq+r\\&|r|<|n|\end{aligned}}

(1)

This still leaves a sign ambiguity if the remainder is non-zero: two possible choices for the remainder occur, one negative and the other positive; that choice determines which of the two consecutive quotients must be used to satisfy equation (1). In number theory, the positive remainder is always chosen, but in computing, programming languages choose depending on the language and the signs of $a$ or $n$ .^[a] Standard Pascal and ALGOL 68, for example, give a positive remainder (or 0) even for negative divisors, and some programming languages, such as C90, leave it to the implementation when either of $n$ or $a$ is negative (see the table under § In programming languages for details). $a$ modulo 0 is undefined in most systems, although some do define it as $a$ .

Quotient ( $q$ ) and remainder ( $r$ ) as functions of dividend ( $a$ ), using truncated division

Many implementations use truncated division, for which the quotient is defined by

$q=\operatorname {trunc} \left({\frac {a}{n}}\right)$

where $\operatorname {trunc}$ is the integral part function (rounding toward zero), i.e. the truncation to zero significant digits. Thus according to equation (1), the remainder has the same sign as the dividend a so can take $2| n | - 1$ values:

$r=a-n\operatorname {trunc} \left({\frac {a}{n}}\right)$
Quotient and remainder using floored division

Donald Knuth^[3] promotes floored division, for which the quotient is defined by

$q=\left\lfloor {\frac {a}{n}}\right\rfloor$

where ⌊⌋ is the floor function (rounding down). Thus according to equation (1), the remainder has the same sign as the divisor n:

$r=a-n\left\lfloor {\frac {a}{n}}\right\rfloor$
Quotient and remainder using Euclidean division

Raymond T. Boute^[4] promotes Euclidean division, for which the quotient is defined by

$q=\operatorname {sgn}(n)\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor ={\begin{cases}\left\lfloor {\frac {a}{n}}\right\rfloor &{\text{if }}n>0\\\left\lceil {\frac {a}{n}}\right\rceil &{\text{if }}n<0\\\end{cases}}$

where $sgn$ is the sign function, ⌊⌋ is the floor function (rounding down), and ⌈⌉ is the ceiling function (rounding up). Thus according to equation (1), the remainder is non negative:

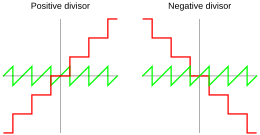
$r=a-|n|\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor$
Quotient and remainder using rounded division

Common Lisp and IEEE 754 use rounded division, for which the quotient is defined by

$q=\operatorname {round} \left({\frac {a}{n}}\right)$

where $round$ is the round function (rounding half to even). Thus according to equation (1), the remainder falls between $-{\frac {n}{2}}$ and ${\frac {n}{2}}$ , and its sign depends on which side of zero it falls to be within these boundaries:

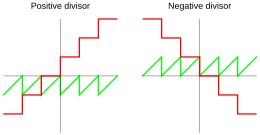
$r=a-n\operatorname {round} \left({\frac {a}{n}}\right)$
Quotient and remainder using ceiling division

Common Lisp also uses ceiling division, for which the quotient is defined by

$q=\left\lceil {\frac {a}{n}}\right\rceil$

where ⌈⌉ is the ceiling function (rounding up). Thus according to equation (1), the remainder has the opposite sign of that of the divisor:

$r=a-n\left\lceil {\frac {a}{n}}\right\rceil$

If both the dividend and divisor are positive, then the truncated, floored, and Euclidean definitions agree. If the dividend is positive and the divisor is negative, then the truncated and Euclidean definitions agree. If the dividend is negative and the divisor is positive, then the floored and Euclidean definitions agree. If both the dividend and divisor are negative, then the truncated and floored definitions agree.

As described by Leijen,

Boute argues that Euclidean division is superior to the other ones in terms of regularity and useful mathematical properties, although floored division, promoted by Knuth, is also a good definition. Despite its widespread use, truncated division is shown to be inferior to the other definitions.
— Daan Leijen, Division and Modulus for Computer Scientists^[5]

However, truncated division satisfies the identity $({-a})/b={-(a/b)}=a/({-b})$ .^[6]

Notation

Some calculators have a $mod()$ function button, and many programming languages have a similar function, expressed as $mod(a, n)$ , for example. Some also support expressions that use "%", "mod", or "Mod" as a modulo or remainder operator, such as a % n or a mod n.

For environments lacking a similar function, any of the three definitions above can be used.

Common pitfalls

When the result of a modulo operation has the sign of the dividend (truncated definition), it can lead to surprising mistakes.

For example, to test if an integer is odd, one might be inclined to test if the remainder by 2 is equal to 1:

bool is_odd(int n) {
    return n % 2 == 1;
}

But in a language where modulo has the sign of the dividend, that is incorrect, because when $n$ (the dividend) is negative and odd, $n$ mod 2 returns −1, and the function returns false.

One correct alternative is to test that the remainder is not 0 (because remainder 0 is the same regardless of the signs):

bool is_odd(int n) {
    return n % 2 != 0;
}

Another alternative is to use the fact that for any odd number, the remainder may be either 1 or −1:

bool is_odd(int n) {
    return n % 2 == 1 || n % 2 == -1;
}

A simpler alternative is to treat the result of n % 2 as if it is a boolean value, where any non-zero value is true:

bool is_odd(int n) {
    return n % 2;
}

Performance issues

Modulo operations might be implemented such that a division with a remainder is calculated each time. For special cases, on some hardware, faster alternatives exist. For example, the modulo of powers of 2 can alternatively be expressed as a bitwise AND operation (assuming $x$ is a positive integer, or using a non-truncating definition):

x % 2ⁿ == x & (2ⁿ - 1)

Examples:

x % 2 == x & 1

x % 4 == x & 3

x % 8 == x & 7

In devices and software that implement bitwise operations more efficiently than modulo, these alternative forms can result in faster calculations.^[7]

Compiler optimizations may recognize expressions of the form expression % constant where constant is a power of two and automatically implement them as expression & (constant-1), allowing the programmer to write clearer code without compromising performance. This simple optimization is not possible for languages in which the result of the modulo operation has the sign of the dividend (including C), unless the dividend is of an unsigned integer type. This is because, if the dividend is negative, the modulo will be negative, whereas expression & (constant-1) will always be positive. For these languages, the equivalence x % 2ⁿ == x < 0 ? x | ~(2ⁿ - 1) : x & (2ⁿ - 1) has to be used instead, expressed using bitwise OR, NOT and AND operations.

Optimizations for general constant-modulus operations also exist by calculating the division first using the constant-divisor optimization.

Properties (identities)

Some modulo operations can be factored or expanded similarly to other mathematical operations. This may be useful in cryptography proofs, such as the Diffie–Hellman key exchange. The properties involving multiplication, division, and exponentiation generally require that $a$ and $n$ are integers.

Identity:
- $(a mod n) mod n = a mod n$ .
- $n x mod n = 0$ for all positive integer values of $x$ .
- If $p$ is a prime number which is not a divisor of $b$ , then $ab p -1 mod p = a mod p$ , due to Fermat's little theorem.
Inverse:
- $mod n = 0$ .
- $b -1 mod n$ denotes the modular multiplicative inverse, which is defined if and only if $b$ and $n$ are relatively prime, which is the case when the left hand side is defined: $mod n = 1$ .
Distributive:
- $(a + b) mod n = mod n$ .
- $ab mod n = mod n$ .
Division (definition): $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}a/b mod n = mod n$ , when the right hand side is defined (that is when $b$ and $n$ are coprime), and undefined otherwise.
Inverse multiplication: $mod n = a mod n$ .

In programming languages

Zdroj:https://en.wikipedia.org?pojem=Modulo_operator
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

Navigácia: Veda >

Analytika
Antropológia
Aplikované vedy
Bibliometria
Dejiny vedy
Encyklopédie
Filozofia vedy
Forenzné vedy
Humanitné vedy
Knižničná veda
Kryogenika
Kryptológia
Kulturológia
Literárna veda
Medzidisciplinárne oblasti
Metódy kvantitatívnej analýzy
Metavedy
Metodika

Metodológia vedy
Náboženstvo a veda
Náučná literatúra
Podvody vo vede
Popularizácia vedy
Potravinárstvo
Prírodné vedy
Pseudoveda
Scientometria
Spoločenské vedy
Teórie
Teatrológia
Technické vedy
Technika
Terminológia
Umenie
Výskum

Veda
Veda a technika podľa štátu
Veda a technika podľa kontinentu
Veda a technika podľa roka
Veda v kozme
Vedci
Vedecká literatúra
Vedecké databázy
Vedecké experimenty
Vedecké konferencie
Vedecké metódy
Vedecké ocenenia
Vedecké organizácie
Vedecké parky
Vedeckí spisovatelia
Vzdelávanie
Záhady

Príbuzné výrazy:

Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok.
Podrobnejšie informácie nájdete na stránke Podmienky použitia.

Modulo operators in various programming languages
Language	Operator	Integer	Floating-point	Definition
ABAP	`MOD`	Yes	Yes	Euclidean
ActionScript	`%`	Yes	No	Truncated
Ada	`mod`	Yes	No	Floored^[8]
Ada	`rem`	Yes	No	Truncated^[8]
ALGOL 68	`÷×`, `mod`	Yes	No	Euclidean
AMPL	`mod`	Yes	No	Truncated
APL	`\|`^[b]	Yes	Yes	Floored
AppleScript	`mod`	Yes	No	Truncated
AutoLISP	`(rem d n)`	Yes	No	Truncated
AWK	`%`	Yes	No	Truncated
bash	`%`	Yes	No	Truncated
BASIC	`Mod`	Yes	No	Varies by implementation
bc	`%`	Yes	No	Truncated
C C++	`%`, `div`	Yes	No

[1]

[2]

[a]

[3]

[4]

[5]

[6]

[7]

[8]

[b]