Moment of inertia factor

In planetary sciences, the moment of inertia factor or normalized polar moment of inertia is a dimensionless quantity that characterizes the radial distribution of mass inside a planet or satellite. Since a moment of inertia has dimensions of mass times length squared, the moment of inertia factor is the coefficient that multiplies these.

Definition

For a planetary body with principal moments of inertia $A<B<C$ , the moment of inertia factor is defined as

{\frac {C}{MR^{2}}}

,

where C is the first principal moment of inertia of the body, M is the mass of the body, and R is the mean radius of the body.^[1]^[2] For a sphere with uniform density, $C/MR^{2}=2/5$ .^{[note 1]}^{[note 2]} For a differentiated planet or satellite, where there is an increase of density with depth, $C/MR^{2}<2/5$ . The quantity is a useful indicator of the presence and extent of a planetary core, because a greater departure from the uniform-density value of 2/5 conveys a greater degree of concentration of dense materials towards the center.

Solar System values

The Sun has by far the lowest moment of inertia factor value among Solar System bodies; it has by far the highest central density (162 g/cm³,^[3]^{[note 3]} compared to ~13 for Earth^[4]^[5]) and a relatively low average density (1.41 g/cm³ versus 5.5 for Earth). Saturn has the lowest value among the gas giants in part because it has the lowest bulk density (0.687 g/cm³).^[6] Ganymede has the lowest moment of inertia factor among solid bodies in the Solar System because of its fully differentiated interior,^[7]^[8] a result in part of tidal heating due to the Laplace resonance,^[9] as well as its substantial component of low density water ice. Callisto is similar in size and bulk composition to Ganymede, but is not part of the orbital resonance and is less differentiated.^[7]^[8] The Moon is thought to have a small core, but its interior is otherwise relatively homogenous.^[10]^[11]

Body	Value	Source	Notes
Sun	0.070	^[3]	Not measured
Mercury	0.346 ± 0.014	^[12]
Venus	0.337 ± 0.024	^[13]
Earth	0.3307	^[14]
Moon	0.3929 ± 0.0009	^[15]
Mars	0.3644 ± 0.0005	^[16]
Ceres	0.36 ± 0.15^{[note 4]}	^[18]	Not measured (range reflects different assumptions for original spin rate^[18])
Jupiter	0.2756 ± 0.0006	^[19]	Not measured (two-layer model calculations constrained by Juno gravity data^[19])
Io	0.37824 ± 0.00022	^[20]	Not measured (Darwin-Radau relation)
Europa	0.346 ± 0.005	^[20]	Not measured (Darwin-Radau relation)
Ganymede	0.3115 ± 0.0028	^[20]	Not measured (Darwin-Radau relation)
Callisto	0.3549 ± 0.0042	^[20]	Not measured (Darwin-Radau relation)
Saturn	0.22	^[21]	Not measured (Darwin-Radau relation)
Enceladus	0.3305 ± 0.0025	^[22]	Not measured (Darwin-Radau relation)
Rhea	0.3911 ± 0.0045	^[23]	Not measured (Darwin-Radau relation)
Titan	0.341	^[24]	Not measured (Darwin-Radau relation)
Uranus	0.23	^[25]	Not measured (approximate solution to Clairaut's equation)
Neptune	0.23	^[25]	Not measured (approximate solution to Clairaut's equation)

Measurement

The polar moment of inertia is traditionally determined by combining measurements of spin quantities (spin precession rate and/or obliquity) with gravity quantities (coefficients of a spherical harmonic representation of the gravity field). These geodetic data usually require an orbiting spacecraft to collect.

Approximation

For bodies in hydrostatic equilibrium, the Darwin–Radau relation can provide estimates of the moment of inertia factor on the basis of shape, spin, and gravity quantities.^[26]

Role in interior models

The moment of inertia factor provides an important constraint for models representing the interior structure of a planet or satellite. At a minimum, acceptable models of the density profile must match the volumetric mass density and moment of inertia factor of the body.

Gallery of internal structure models

The Sun (C/MR² = 0.070)
Saturn (C/MR² = 0.22)
Ganymede (C/MR² = 0.3115)
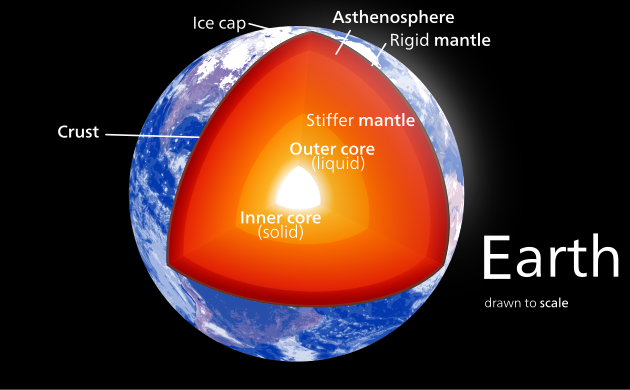
Earth (C/MR² = 0.3307)
Callisto (C/MR² = 0.3549)
The Moon (C/MR² = 0.3929)

Notes

^ For a sphere with uniform density we can calculate the moment of inertia and the mass by integrating over disks from the "south pole" to the "north pole". Using a density of 1, a disk of radius $r$ has a moment of inertia of
$\int _{0}^{r}2\pi r^{3}\ dr={\frac {\pi r^{4}}{2}}$
whereas the mass is
$\int _{0}^{r}2\pi r\ dr=\pi r^{2}$
Letting $r=R\cos \theta$ and integrating over $R\sin \theta$ we get:
${\begin{aligned}{\frac {C}{R^{5}}}&={\frac {\pi }{2}}\int _{-1}^{1}\cos ^{4}\theta \ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-\sin ^{2}\theta )^{2}\ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-2\sin ^{2}\theta +\sin ^{4}\theta )d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(d\sin \theta -{\frac {2}{3}}d\sin ^{3}\theta +{\frac {1}{5}}d\sin ^{5}\theta )\\&={\frac {8}{15}}\pi \end{aligned}}$

${\begin{aligned}{\frac {M}{R^{3}}}&=\pi \int _{-1}^{1}\cos ^{2}\theta \ d\sin \theta \\&=\pi \int _{-1}^{1}(1-\sin ^{2}\theta )d\sin \theta \\&=\pi \int _{-1}^{1}(d\sin \theta -{\frac {1}{3}}d\sin ^{3}\theta )\\&={\frac {4}{3}}\pi \end{aligned}}$
This gives $C/MR^{2}=2/5$ .
^ For several other examples (in which the rotation axis is the axis of symmetry if not otherwise specified), a solid cone has a factor of 3/10; a uniform thin rod (rotating about its center perpendicularly to its axis, so R is length/2) has a factor of 1/3; a hollow cone or a solid cylinder has a factor of 1/2; a hollow sphere has factor of 2/3; a hollow open-ended cylinder has a factor of 1.
^ A star's central density tends to increase over the course of its lifetime, aside from during brief core nuclear fusion ignition events like the helium flash.
^ The value given for Ceres is the mean moment of inertia, which is thought to better represent its interior structure than the polar moment of inertia, due to its high polar flattening.^[17]

References

^ Hubbard, William B. (1984). Planetary interiors. New York, N.Y.: Van Nostrand Reinhold. ISBN 978-0442237042. OCLC 10147326. Zdroj:https://en.wikipedia.org?pojem=Moment_of_inertia_factor
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

Navigácia: Veda >

Analytika
Antropológia
Aplikované vedy
Bibliometria
Dejiny vedy
Encyklopédie
Filozofia vedy
Forenzné vedy
Humanitné vedy
Knižničná veda
Kryogenika
Kryptológia
Kulturológia
Literárna veda
Medzidisciplinárne oblasti
Metódy kvantitatívnej analýzy
Metavedy
Metodika

Metodológia vedy
Náboženstvo a veda
Náučná literatúra
Podvody vo vede
Popularizácia vedy
Potravinárstvo
Prírodné vedy
Pseudoveda
Scientometria
Spoločenské vedy
Teórie
Teatrológia
Technické vedy
Technika
Terminológia
Umenie
Výskum

Veda
Veda a technika podľa štátu
Veda a technika podľa kontinentu
Veda a technika podľa roka
Veda v kozme
Vedci
Vedecká literatúra
Vedecké databázy
Vedecké experimenty
Vedecké konferencie
Vedecké metódy
Vedecké ocenenia
Vedecké organizácie
Vedecké parky
Vedeckí spisovatelia
Vzdelávanie
Záhady

Príbuzné výrazy:

Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok.
Podrobnejšie informácie nájdete na stránke Podmienky použitia.

[3] For a sphere with uniform density we can calculate the moment of inertia and the mass by integrating over disks from the "south pole" to the "north pole". Using a density of 1, a disk of radius $r$ has a moment of inertia of
$\int _{0}^{r}2\pi r^{3}\ dr={\frac {\pi r^{4}}{2}}$
whereas the mass is
$\int _{0}^{r}2\pi r\ dr=\pi r^{2}$
Letting $r=R\cos \theta$ and integrating over $R\sin \theta$ we get:
${\begin{aligned}{\frac {C}{R^{5}}}&={\frac {\pi }{2}}\int _{-1}^{1}\cos ^{4}\theta \ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-\sin ^{2}\theta )^{2}\ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-2\sin ^{2}\theta +\sin ^{4}\theta )d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(d\sin \theta -{\frac {2}{3}}d\sin ^{3}\theta +{\frac {1}{5}}d\sin ^{5}\theta )\\&={\frac {8}{15}}\pi \end{aligned}}$

${\begin{aligned}{\frac {M}{R^{3}}}&=\pi \int _{-1}^{1}\cos ^{2}\theta \ d\sin \theta \\&=\pi \int _{-1}^{1}(1-\sin ^{2}\theta )d\sin \theta \\&=\pi \int _{-1}^{1}(d\sin \theta -{\frac {1}{3}}d\sin ^{3}\theta )\\&={\frac {4}{3}}\pi \end{aligned}}$
This gives $C/MR^{2}=2/5$ .

[4] For several other examples (in which the rotation axis is the axis of symmetry if not otherwise specified), a solid cone has a factor of 3/10; a uniform thin rod (rotating about its center perpendicularly to its axis, so R is length/2) has a factor of 1/3; a hollow cone or a solid cylinder has a factor of 1/2; a hollow sphere has factor of 2/3; a hollow open-ended cylinder has a factor of 1.

[6] A star's central density tends to increase over the course of its lifetime, aside from during brief core nuclear fusion ignition events like the helium flash.

[21] The value given for Ceres is the mean moment of inertia, which is thought to better represent its interior structure than the polar moment of inertia, due to its high polar flattening.^[17]

[Hubbard84-1] Hubbard, William B. (1984). Planetary interiors. New York, N.Y.: Van Nostrand Reinhold. ISBN 978-0442237042. OCLC 10147326. Zdroj:https://en.wikipedia.org?pojem=Moment_of_inertia_factor
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

[1]

[2]

[note 1]

[note 2]

[3]

[note 3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[note 4]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[17]