Opísaná kružnica je kružnica, na ktorej ležia všetky vrcholy rovinného útvaru.

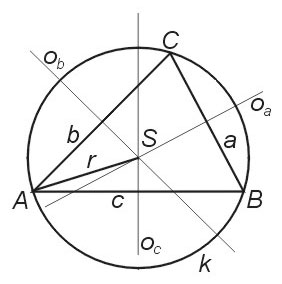
Kružnica opísaná trojuholníku

Stred kružnice opísanej trojuholníku je priesečník osí strán trojuholníka, polomer sa rovná vzdialenosti stredu od ľubovoľného vrcholu. Každému trojuholníku možno opísať kružnicu.

Vlastnosti opísanej kružnice trojuholníka

• Veľkosť polomeru opísanej kružnice určuje vzťah

${\displaystyle r={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}.}$

• Spojnica stredu opísanej kružnice a jednotlivých vrcholov trojuholníka sú kolmé k stranám jeho ortického trojuholníka (tzv. Nagelova veta).
• Kružnica deviatich bodov je rovnako vzdialeným obrazom opísanej kružnice so stredom rovnoľahlosti v ťažisku trojuholníka a koeficientom κ = - 0,5.
• Stredom úsečky spájajúcej stred opísanej kružnice a Lemoinov bod je zároveň stredom prvej Lemoinovej kružnice.

Opísaná kružnica trojuholníka a jej konštrukcia
Opísaná kružnica ${\displaystyle k(S;r)}$
osi strán ${\displaystyle o^{a},o^{b},o^{c}}$
stred kružnice ${\displaystyle S\in \cap o^{a}\cap o^{b}\cap o^{c}}$
polomer kružnice ${\displaystyle r=|AS|}$

Simsonova priamka

Opísaná kružnica a Simsonova priamka

Ak z ľubovoľného bodu X opísanej kružnice vedieme kolmicu k jednotlivým stranám, päty kolmíc ležia na priamke. Nazýva sa Simsonova priamka. Ak tento bod X spojíme s ortocentrom (priesečník výšok trojuholníka), potom Simsonova priamka prechádza stredom tejto úsečky. Simsonova priamka sa volá podľa anglického matematika Roberta Simsona (1687-1768). Niekedy sa označuje aj ako Wallaceova priamka.

Popis obrázka

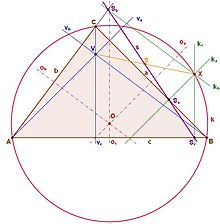
Opísaná kružnica a Simsonova priamka:

• ABC
• a, b, c – strany
• o_a, o_b, o_c - osi strán,
• O – priesečník osí strán (stred opísanej kružnice),
• X – ľubovoľný bod, ležiaci na opísanej kružnici
• k_a, k_b, k_c – kolmica na strany, vedená z bodu X
• S_a, S_b, S_c – päty kolmíc k_a, k_b, k_c
• s – Simsonova priamka
• v_a, v_b, v_c – výšky,
• V – priesečník výšok (ortocentrum)
• S – stred úsečky VX

Tálesova kružnica

Bližšie informácie v hlavnom článku: Tálesova veta

Opísaná kružnica pravouhlého trojuholníka sa nazýva Tálesova kružnica. Stred Tálesovej kružnice leží v strede prepony trojuholníka. Ak máme napr. trojuholník ABC, hovoríme, že Tálesova kružnica je zostrojená nad priemerom AB.

Pre každú úsečku AB platí, že Tálesova kružnica zostrojená nad priemerom AB (s vybraním bodov A a B) je množinou vrcholov C všetkých pravouhlých trojuholníkov ABC s preponou AB.

Kružnica opísaná štvoruholníku

Stred opísanej kružnice štvorca alebo obdĺžnika je priesečník uhlopriečok daného rovnobežníka.

Pozri aj

• Vpísaná kružnica
• Pripísaná kružnica
• Lemoinova kružnica

Zdroje

Tento článok je čiastočný alebo úplný preklad článku Kružnice opsaná na českej Wikipédii.

• Kružnica opísaná trojuholníku

Literatúra

• ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha : Nakladatelství technické literatury, 1988.