A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra:
| Tetrahedron | Cube | Octahedron | Dodecahedron | Icosahedron |
| Four faces | Six faces | Eight faces | Twelve faces | Twenty faces |

|

|

|

|

|
Geometers have studied the Platonic solids for thousands of years.[1] They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the Timaeus, that the classical elements were made of these regular solids.[2]
History
The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 vertices of the dodecahedron, and the arrangement of the knobs was not always symmetric.[3]
The ancient Greeks studied the Platonic solids extensively. Some sources (such as Proclus) credit Pythagoras with their discovery. Other evidence suggests that he may have only been familiar with the tetrahedron, cube, and dodecahedron and that the discovery of the octahedron and icosahedron belong to Theaetetus, a contemporary of Plato. In any case, Theaetetus gave a mathematical description of all five and may have been responsible for the first known proof that no other convex regular polyhedra exist.
The Platonic solids are prominent in the philosophy of Plato, their namesake. Plato wrote about them in the dialogue Timaeus c. 360 B.C. in which he associated each of the four classical elements (earth, air, water, and fire) with a regular solid. Earth was associated with the cube, air with the octahedron, water with the icosahedron, and fire with the tetrahedron.
Of the fifth Platonic solid, the dodecahedron, Plato obscurely remarked, "...the god used for arranging the constellations on the whole heaven". Aristotle added a fifth element, aither (aether in Latin, "ether" in English) and postulated that the heavens were made of this element, but he had no interest in matching it with Plato's fifth solid.[4]
Euclid completely mathematically described the Platonic solids in the Elements, the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no further convex regular polyhedra. Andreas Speiser has advocated the view that the construction of the five regular solids is the chief goal of the deductive system canonized in the Elements.[5] Much of the information in Book XIII is probably derived from the work of Theaetetus.
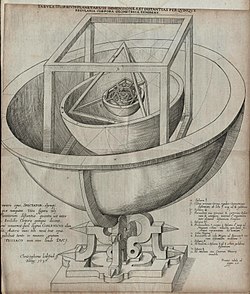
In the 16th century, the German astronomer Johannes Kepler attempted to relate the five extraterrestrial planets known at that time to the five Platonic solids. In Mysterium Cosmographicum, published in 1596, Kepler proposed a model of the Solar System in which the five solids were set inside one another and separated by a series of inscribed and circumscribed spheres. Kepler proposed that the distance relationships between the six planets known at that time could be understood in terms of the five Platonic solids enclosed within a sphere that represented the orbit of Saturn. The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube, thereby dictating the structure of the solar system and the distance relationships between the planets by the Platonic solids. In the end, Kepler's original idea had to be abandoned, but out of his research came his three laws of orbital dynamics, the first of which was that the orbits of planets are ellipses rather than circles, changing the course of physics and astronomy.[6] He also discovered the Kepler solids, which are two nonconvex regular polyhedra.
Cartesian coordinates
For Platonic solids centered at the origin, simple Cartesian coordinates of the vertices are given below. The Greek letter φ is used to represent the golden ratio 1 + √5/2 ≈ 1.6180.
| Figure | Tetrahedron | Octahedron | Cube | Icosahedron | Dodecahedron | |||
|---|---|---|---|---|---|---|---|---|
| Faces | 4 | 8 | 6 | 20 | 12 | |||
| Vertices | 4 | 6 (2 × 3) | 8 | 12 (4 × 3) | 20 (8 + 4 × 3) | |||
| Position | 1 | 2 | 1 | 2 | 1 | 2 | ||
| Vertex coordinates |
(1, 1, 1) (1, −1, −1) (−1, 1, −1) (−1, −1, 1) |
(−1, −1, −1) (−1, 1, 1) ( 1, −1, 1) ( 1, 1, −1) |
(±1, 0, 0) ( 0, ±1, 0) ( 0, 0, ±1) |
(±1, ±1, ±1) | ( 0, ±1, ±φ) (±1, ±φ, 0) (±φ, 0, ±1) |
( 0, ±φ, ±1) (±φ, ±1, 0) (±1, 0, ±φ) |
(±1, ±1, ±1) ( 0, ±1/φ, ±φ) (±1/φ, ±φ, 0) (±φ, 0, ±1/φ) |
(±1, ±1, ±1) ( 0, ±φ, ±1/φ) (±φ, ±1/φ, 0) (±1/φ, 0, ±φ) |
The coordinates for the tetrahedron, dodecahedron, and icosahedron are given in two positions such that each can be deduced from the other: in the case of the tetrahedron, by changing all coordinates of sign (central symmetry), or, in the other cases, by exchanging two coordinates (reflection with respect to any of the three diagonal planes).
These coordinates reveal certain relationships between the Platonic solids: the vertices of the tetrahedron represent half of those of the cube, as {4,3} or ![]()
![]()
![]()
![]()
![]() , one of two sets of 4 vertices in dual positions, as h{4,3} or
, one of two sets of 4 vertices in dual positions, as h{4,3} or ![]()
![]()
![]()
![]()
![]() . Both tetrahedral positions make the compound stellated octahedron.
. Both tetrahedral positions make the compound stellated octahedron.
The coordinates of the icosahedron are related to two alternated sets of coordinates of a nonuniform truncated octahedron, t{3,4} or ![]()
![]()
![]()
![]()
![]() , also called a snub octahedron, as s{3,4} or
, also called a snub octahedron, as s{3,4} or ![]()
![]()
![]()
![]()
![]() , and seen in the compound of two icosahedra.
, and seen in the compound of two icosahedra.
Eight of the vertices of the dodecahedron are shared with the cube. Completing all orientations leads to the compound of five cubes.
Combinatorial properties
A convex polyhedron is a Platonic solid if and only if all three of the following requirements are met.
- All of its faces are congruent convex regular polygons.
- None of its faces intersect except at their edges.
- The same number of faces meet at each of its vertices.
Each Platonic solid can therefore be assigned a pair {p, q} of integers, where p is the number of edges (or, equivalently, vertices) of each face, and q is the number of faces (or, equivalently, edges) that meet at each vertex. This pair {p, q}, called the Schläfli symbol, gives a combinatorial description of the polyhedron. The Schläfli symbols of the five Platonic solids are given in the table below.
| Polyhedron | Vertices | Edges | Faces | Schläfli symbol | Vertex configuration | |
|---|---|---|---|---|---|---|
| tetrahedron | 4 | 6 | 4 | {3, 3} | 3.3.3 | |
| cube | 
|
8 | 12 | 6 | {4, 3} | 4.4.4 |
| octahedron | 
|
6 | 12 | 8 | {3, 4} | 3.3.3.3 |
| dodecahedron | 
|
20 | 30 | 12 | {5, 3} | 5.5.5 |
| icosahedron | 12 | 30 | 20 | {3, 5} | 3.3.3.3.3 | |
All other combinatorial information about these solids, such as total number of vertices (V), edges (E), and faces (F), can be determined from p and q. Since any edge joins two vertices and has two adjacent faces we must have:
The other relationship between these values is given by Euler's formula:
This can be proved in many ways. Together these three relationships completely determine V, E, and F:
Swapping p and q interchanges F and V while leaving E unchanged. For a geometric interpretation of this property, see § Dual polyhedra.
As a configuration
The elements of a polyhedron can be expressed in a configuration matrix. The rows and columns correspond to vertices, edges, and faces. The diagonal numbers say how many of each element occur in the whole polyhedron. The nondiagonal numbers say how many of the column's element occur in or at the row's element. Dual pairs of polyhedra have their configuration matrices rotated 180 degrees from each other.[7]
| {p,q} | Platonic configurations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group order: g = 8pq/(4 − (p − 2)(q − 2)) |
g = 24 | g = 48 | g = 120 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Classification
The classical result is that only five convex regular polyhedra exist. Two common arguments below demonstrate no more than five Platonic solids can exist, but positively demonstrating the existence of any given solid is a separate question—one that requires an explicit construction.
Geometric proof
{3,3} Defect 180° |
 {3,4} Defect 120° |
 {3,5} Defect 60° |
 {3,6} Defect 0° |
 {4,3} Defect 90° |
 {4,4} Defect 0° |
 {5,3} Defect 36° |
 {6,3} Defect 0° |
| A vertex needs at least 3 faces, and an angle defect. A 0° angle defect will fill the Euclidean plane with a regular tiling. By Descartes' theorem, the number of vertices is 720°/defect. | |||
The following geometric argument is very similar to the one given by Euclid in the Elements:
- Each vertex of the solid must be a vertex for at least three faces.
- At each vertex of the solid, the total, among the adjacent faces, of the angles between their respective adjacent sides must be strictly less than 360°. The amount less than 360° is called an angle defect.
- Regular polygons of six or more sides have only angles of 120° or more, so the common face must be the triangle, square, or pentagon. For these different shapes of faces the following holds:
- Triangular faces
- Each vertex of a regular triangle is 60°, so a shape may have three, four, or five triangles meeting at a vertex; these are the tetrahedron, octahedron, and icosahedron respectively.
- Square faces
- Each vertex of a square is 90°, so there is only one arrangement possible with three faces at a vertex, the cube.
- Pentagonal faces
- Each vertex is 108°; again, only one arrangement of three faces at a vertex is possible, the dodecahedron.
Topological proof
A purely topological proof can be made using only combinatorial information about the solids. The key is Euler's observation that V − E + F = 2, and the fact that pF = 2E = qV, where p stands for the number of edges of each face and q for the number of edges meeting at each vertex. Combining these equations one obtains the equation

Antropológia
Aplikované vedy
Bibliometria
Dejiny vedy
Encyklopédie
Filozofia vedy
Forenzné vedy
Humanitné vedy
Knižničná veda
Kryogenika
Kryptológia
Kulturológia
Literárna veda
Medzidisciplinárne oblasti
Metódy kvantitatívnej analýzy
Metavedy
Metodika
Text je dostupný za podmienok Creative
Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších
podmienok.
Podrobnejšie informácie nájdete na stránke Podmienky
použitia.
www.astronomia.sk | www.biologia.sk | www.botanika.sk | www.dejiny.sk | www.economy.sk | www.elektrotechnika.sk | www.estetika.sk | www.farmakologia.sk | www.filozofia.sk | Fyzika | www.futurologia.sk | www.genetika.sk | www.chemia.sk | www.lingvistika.sk | www.politologia.sk | www.psychologia.sk | www.sexuologia.sk | www.sociologia.sk | www.veda.sk I www.zoologia.sk