Radiation pressure (also known as light pressure) is mechanical pressure exerted upon a surface due to the exchange of momentum between the object and the electromagnetic field. This includes the momentum of light or electromagnetic radiation of any wavelength that is absorbed, reflected, or otherwise emitted (e.g. black-body radiation) by matter on any scale (from macroscopic objects to dust particles to gas molecules).^[1][2][3] The associated force is called the radiation pressure force, or sometimes just the force of light.

The forces generated by radiation pressure are generally too small to be noticed under everyday circumstances; however, they are important in some physical processes and technologies. This particularly includes objects in outer space, where it is usually the main force acting on objects besides gravity, and where the net effect of a tiny force may have a large cumulative effect over long periods of time. For example, had the effects of the Sun's radiation pressure on the spacecraft of the Viking program been ignored, the spacecraft would have missed Mars orbit by about 15,000 km (9,300 mi).^[4] Radiation pressure from starlight is crucial in a number of astrophysical processes as well. The significance of radiation pressure increases rapidly at extremely high temperatures and can sometimes dwarf the usual gas pressure, for instance, in stellar interiors and thermonuclear weapons. Furthermore, large lasers operating in space have been suggested as a means of propelling sail craft in beam-powered propulsion.

Radiation pressure forces are the bedrock of laser technology and the branches of science that rely heavily on lasers and other optical technologies. That includes, but is not limited to, biomicroscopy (where light is used to irradiate and observe microbes, cells, and molecules), quantum optics, and optomechanics (where light is used to probe and control objects like atoms, qubits and macroscopic quantum objects). Direct applications of the radiation pressure force in these fields are, for example, laser cooling (the subject of the 1997 Nobel Prize in Physics),^[5] quantum control of macroscopic objects and atoms (2012 Nobel Prize in Physics),^[6] interferometry (2017 Nobel Prize in Physics)^[7] and optical tweezers (2018 Nobel Prize in Physics).^[8]

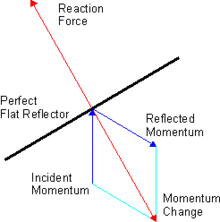
Radiation pressure can equally well be accounted for by considering the momentum of a classical electromagnetic field or in terms of the momenta of photons, particles of light. The interaction of electromagnetic waves or photons with matter may involve an exchange of momentum. Due to the law of conservation of momentum, any change in the total momentum of the waves or photons must involve an equal and opposite change in the momentum of the matter it interacted with (Newton's third law of motion), as is illustrated in the accompanying figure for the case of light being perfectly reflected by a surface. This transfer of momentum is the general explanation for what we term radiation pressure.

Discovery

Johannes Kepler put forward the concept of radiation pressure in 1619 to explain the observation that a tail of a comet always points away from the Sun.^[9]

The assertion that light, as electromagnetic radiation, has the property of momentum and thus exerts a pressure upon any surface that is exposed to it was published by James Clerk Maxwell in 1862, and proven experimentally by Russian physicist Pyotr Lebedev in 1900^[10] and by Ernest Fox Nichols and Gordon Ferrie Hull in 1901.^[11] The pressure is very small, but can be detected by allowing the radiation to fall upon a delicately poised vane of reflective metal in a Nichols radiometer (this should not be confused with the Crookes radiometer, whose characteristic motion is not caused by radiation pressure but by air flow caused by temperature differentials.)

Theory

Radiation pressure can be viewed as a consequence of the conservation of momentum given the momentum attributed to electromagnetic radiation. That momentum can be equally well calculated on the basis of electromagnetic theory or from the combined momenta of a stream of photons, giving identical results as is shown below.

Radiation pressure from momentum of an electromagnetic wave

According to Maxwell's theory of electromagnetism, an electromagnetic wave carries momentum. Momentum will be transferred to any surface it strikes that absorbs or reflects the radiation.

Consider the momentum transferred to a perfectly absorbing (black) surface. The energy flux (irradiance) of a plane wave is calculated using the Poynting vector ${\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} }$, which is the cross product of the electric field vector E and the magnetic field's auxiliary field vector (or magnetizing field) H. The magnitude, denoted by S, divided by the speed of light is the density of the linear momentum per unit area (pressure) of the electromagnetic field. So, dimensionally, the Poynting vector is S = power/area = rate of doing work/area = ΔF/Δt Δx/area, which is the speed of light, c = Δx / Δt, times pressure, ΔF / area. That pressure is experienced as radiation pressure on the surface:

$${\displaystyle P_{\text{incident}}={\frac {\langle S\rangle }{c}}={\frac {I_{f}}{c}}}$$

where ${\displaystyle P}$ is pressure (usually in pascals), ${\displaystyle I_{f}}$ is the incident irradiance (usually in W/m²) and ${\displaystyle c}$ is the speed of light in vacuum. Here, 1/c ≈ 3.34 N/GW.

If the surface is planar at an angle α to the incident wave, the intensity across the surface will be geometrically reduced by the cosine of that angle and the component of the radiation force against the surface will also be reduced by the cosine of α, resulting in a pressure:

$${\displaystyle P_{\text{incident}}={\frac {I_{f}}{c}}\cos ^{2}\alpha }$$

The momentum from the incident wave is in the same direction of that wave. But only the component of that momentum normal to the surface contributes to the pressure on the surface, as given above. The component of that force tangent to the surface is not called pressure.^[12]

Radiation pressure from reflection

The above treatment for an incident wave accounts for the radiation pressure experienced by a black (totally absorbing) body. If the wave is specularly reflected, then the recoil due to the reflected wave will further contribute to the radiation pressure. In the case of a perfect reflector, this pressure will be identical to the pressure caused by the incident wave:

$${\displaystyle P_{\text{emitted}}={\frac {I_{f}}{c}}}$$

thus doubling the net radiation pressure on the surface:

$${\displaystyle P_{\text{net}}=P_{\text{incident}}+P_{\text{emitted}}=2{\frac {I_{f}}{c}}}$$

For a partially reflective surface, the second term must be multiplied by the reflectivity (also known as reflection coefficient of intensity), so that the increase is less than double. For a diffusely reflective surface, the details of the reflection and geometry must be taken into account, again resulting in an increased net radiation pressure of less than double.

Radiation pressure by emission

Just as a wave reflected from a body contributes to the net radiation pressure experienced, a body that emits radiation of its own (rather than reflected) obtains a radiation pressure again given by the irradiance of that emission in the direction normal to the surface I_e:

$${\displaystyle P_{\text{emitted}}={\frac {I_{\text{e}}}{c}}}$$

The emission can be from black-body radiation or any other radiative mechanism. Since all materials emit black-body radiation (unless they are totally reflective or at absolute zero), this source for radiation pressure is ubiquitous but usually tiny. However, because black-body radiation increases rapidly with temperature (as the fourth power of temperature, given by the Stefan–Boltzmann law), radiation pressure due to the temperature of a very hot object (or due to incoming black-body radiation from similarly hot surroundings) can become significant. This is important in stellar interiors.

Radiation pressure in terms of photons

Electromagnetic radiation can be viewed in terms of particles rather than waves; these particles are known as photons. Photons do not have a rest-mass; however, photons are never at rest (they move at the speed of light) and acquire a momentum nonetheless which is given by:

$${\displaystyle p={\dfrac {h}{\lambda }}={\frac {E_{p}}{c}},}$$

$${\displaystyle E_{p}=h\nu ={\frac {hc}{\lambda }}}$$

The radiation pressure again can be seen as the transfer of each photon's momentum to the opaque surface, plus the momentum due to a (possible) recoil photon for a (partially) reflecting surface. Since an incident wave of irradiance I_f over an area A has a power of I_fA, this implies a flux of I_f/E_p photons per second per unit area striking the surface. Combining this with the above expression for the momentum of a single photon, results in the same relationships between irradiance and radiation pressure described above using classical electromagnetics. And again, reflected or otherwise emitted photons will contribute to the net radiation pressure identically.

Compression in a uniform radiation field

In general, the pressure of electromagnetic waves can be obtained from the vanishing of the trace of the electromagnetic stress tensor: since this trace equals 3P − u, we get

$${\displaystyle P={\frac {u}{3}},}$$

This can also be shown in the specific case of the pressure exerted on surfaces of a body in thermal equilibrium with its surroundings, at a temperature T: the body will be surrounded by a uniform radiation field described by the Planck black-body radiation law and will experience a compressive pressure due to that impinging radiation, its reflection, and its own black-body emission. From that it can be shown that the resulting pressure is equal to one third of the total radiant energy per unit volume in the surrounding space.^{[13][14][15][16]}

By using Stefan–Boltzmann law, this can be expressed as

$${\displaystyle P_{\text{compress}}={\frac {u}{3}}={\frac {4\sigma }{3c}}T^{4},}$$

where ${\displaystyle \sigma }$ is the Stefan–Boltzmann constant.

Solar radiation pressure

Solar radiation pressure is due to the Sun's radiation at closer distances, thus especially within the Solar System. (The radiation pressure of sunlight on Earth is very small: it is equivalent to that exerted by about a milligram on an area of 1 square metre, or 10 μN/m², or 10⁻¹⁰ atmospheres.)^{[citation needed]} While it acts on all objects, its net effect is generally greater on smaller bodies, since they have a larger ratio of surface area to mass. All spacecraft experience such a pressure, except when they are behind the shadow of a larger orbiting body.

Solar radiation pressure on objects near the Earth may be calculated using the Sun's irradiance at 1 AU, known as the solar constant, or G_SC, whose value is set at 1361 W/m² as of 2011.^[17]

All stars have a spectral energy distribution that depends on their surface temperature. The distribution is approximately that of black-body radiation. This distribution must be taken into account when calculating the radiation pressure or identifying reflector materials for optimizing a solar sail, for instance.

Momentary or hours long solar pressures can indeed escalate due to release of solar flares and coronal mass ejections, but effects remain essentially immeasureable in relation to Earth's orbit. However these pressures persist over eons, such that cumulatively having produced a measureable movement on the Earth-Moon system's orbit.

Pressures of absorption and reflection

Solar radiation pressure at the Earth's distance from the Sun, may be calculated by dividing the solar constant G_SC (above) by the speed of light c. For an absorbing sheet facing the Sun, this is simply:^[18]

$${\displaystyle P={\frac {G_{\text{SC}}}{c}}\approx 4.5\cdot 10^{-6}~{\text{Pa}}=4.5~\mu {\text{Pa}}.}$$

This result is in pascals, equivalent to N/m² (newtons per square meter). For a sheet at an angle α to the Sun, the effective area A of a sheet is reduced by a geometrical factor resulting in a force in the direction of the sunlight of:

$${\displaystyle F={\frac {G_{\text{SC}}}{c}}(A\cos \alpha ).}$$

To find the component of this force normal to the surface, another cosine factor must be applied resulting in a pressure P on the surface of:

$${\displaystyle P={\frac {F\cos \alpha }{A}}={\frac {G_{\text{SC}}}{c}}\cos ^{2}\alpha .}$$

Note, however, that in order to account for the net effect of solar radiation on a spacecraft for instance, one would need to consider the total force (in the direction away from the Sun) given by the preceding equation, rather than just the component normal to the surface that we identify as "pressure".

The solar constant is defined for the Sun's radiation at the distance to the Earth, also known as one astronomical unit (au). Consequently, at a distance of R astronomical units (R thus being dimensionless), applying the inverse-square law, we would find: