This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Reaction engine" – news · newspapers · books · scholar · JSTOR (June 2008) (Learn how and when to remove this message)

A reaction engine is an engine or motor that produces thrust by expelling reaction mass (reaction propulsion),^[1] in accordance with Newton's third law of motion. This law of motion is commonly paraphrased as: "For every action force there is an equal, but opposite, reaction force."

Examples include jet engines, rocket engines, pump-jets, and more uncommon variations such as Hall effect thrusters, ion drives, mass drivers, and nuclear pulse propulsion.

Discovery

The discovery of the reaction engine has been attributed to the Romanian inventor Alexandru Ciurcu and to the French journalist Just Buisson [fr; ro].^[2]

Energy use

Propulsive efficiency

For all reaction engines that carry on-board propellant (such as rocket engines and electric propulsion drives) some energy must go into accelerating the reaction mass. Every engine wastes some energy, but even assuming 100% efficiency, the engine needs energy amounting to

${\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}MV_{e}^{2}}$

(where M is the mass of propellent expended and ${\displaystyle V_{e}}$ is the exhaust velocity), which is simply the energy to accelerate the exhaust.

Comparing the rocket equation (which shows how much energy ends up in the final vehicle) and the above equation (which shows the total energy required) shows that even with 100% engine efficiency, certainly not all energy supplied ends up in the vehicle – some of it, indeed usually most of it, ends up as kinetic energy of the exhaust.

If the specific impulse (${\displaystyle I_{sp}}$) is fixed, for a mission delta-v, there is a particular ${\displaystyle I_{sp}}$ that minimises the overall energy used by the rocket. This comes to an exhaust velocity of about ⅔ of the mission delta-v (see the energy computed from the rocket equation). Drives with a specific impulse that is both high and fixed such as Ion thrusters have exhaust velocities that can be enormously higher than this ideal, and thus end up powersource limited and give very low thrust. Where the vehicle performance is power limited, e.g. if solar power or nuclear power is used, then in the case of a large ${\displaystyle v_{e}}$ the maximum acceleration is inversely proportional to it. Hence the time to reach a required delta-v is proportional to ${\displaystyle v_{e}}$. Thus the latter should not be too large.

On the other hand, if the exhaust velocity can be made to vary so that at each instant it is equal and opposite to the vehicle velocity then the absolute minimum energy usage is achieved. When this is achieved, the exhaust stops in space ^{[NB 1]} and has no kinetic energy; and the propulsive efficiency is 100% all the energy ends up in the vehicle (in principle such a drive would be 100% efficient, in practice there would be thermal losses from within the drive system and residual heat in the exhaust). However, in most cases this uses an impractical quantity of propellant, but is a useful theoretical consideration.

Some drives (such as VASIMR or electrodeless plasma thruster) actually can significantly vary their exhaust velocity. This can help reduce propellant usage and improve acceleration at different stages of the flight. However the best energetic performance and acceleration is still obtained when the exhaust velocity is close to the vehicle speed. Proposed ion and plasma drives usually have exhaust velocities enormously higher than that ideal (in the case of VASIMR the lowest quoted speed is around 15 km/s compared to a mission delta-v from high Earth orbit to Mars of about 4 km/s).

For a mission, for example, when launching from or landing on a planet, the effects of gravitational attraction and any atmospheric drag must be overcome by using fuel. It is typical to combine the effects of these and other effects into an effective mission delta-v. For example, a launch mission to low Earth orbit requires about 9.3–10 km/s delta-v. These mission delta-vs are typically numerically integrated on a computer.

Cycle efficiency

All reaction engines lose some energy, mostly as heat.

Different reaction engines have different efficiencies and losses. For example, rocket engines can be up to 60–70% energy efficient in terms of accelerating the propellant. The rest is lost as heat and thermal radiation, primarily in the exhaust.

Oberth effect

Reaction engines are more energy efficient when they emit their reaction mass when the vehicle is travelling at high speed.

This is because the useful mechanical energy generated is simply force times distance, and when a thrust force is generated while the vehicle moves, then:

${\displaystyle E=F\times d\;}$

where F is the force and d is the distance moved.

Dividing by length of time of motion we get:

${\displaystyle {\frac {E}{t}}=P={\frac {F\times d}{t}}=F\times v}$

Hence:

${\displaystyle P=F\times v\;}$

where P is the useful power and v is the speed.

Hence, v should be as high as possible, and a stationary engine does no useful work.^{[NB 2]}

Delta-v and propellant

Exhausting the entire usable propellant of a spacecraft through the engines in a straight line in free space would produce a net velocity change to the vehicle; this number is termed delta-v (${\displaystyle \Delta v}$).

If the exhaust velocity is constant then the total ${\displaystyle \Delta v}$ of a vehicle can be calculated using the rocket equation, where M is the mass of propellant, P is the mass of the payload (including the rocket structure), and ${\displaystyle v_{e}}$ is the velocity of the rocket exhaust. This is known as the Tsiolkovsky rocket equation:

${\displaystyle \Delta v=v_{e}\ln \left({\frac {M+P}{P}}\right).}$

For historical reasons, as discussed above, ${\displaystyle v_{e}}$ is sometimes written as

${\displaystyle v_{e}=I_{\text{sp}}g_{0}}$

where ${\displaystyle I_{\text{sp}}}$ is the specific impulse of the rocket, measured in seconds, and ${\displaystyle g_{0}}$ is the gravitational acceleration at sea level.

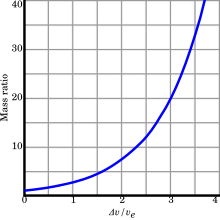
For a high delta-v mission, the majority of the spacecraft's mass needs to be reaction mass. Because a rocket must carry all of its reaction mass, most of the initially-expended reaction mass goes towards accelerating reaction mass rather than payload. If the rocket has a payload of mass P, the spacecraft needs to change its velocity by ${\displaystyle \Delta v}$, and the rocket engine has exhaust velocity v_e, then the reaction mass M which is needed can be calculated using the rocket equation and the formula for ${\displaystyle I_{\text{sp}}}$:

${\displaystyle M=P\left(e^{\frac {\Delta v}{v_{e}}}-1\right).}$

For ${\displaystyle \Delta v}$ much smaller than v_e, this equation is roughly linear, and little reaction mass is needed. If ${\displaystyle \Delta v}$ is comparable to v_e, then there needs to be about twice as much fuel as combined payload and structure (which includes engines, fuel tanks, and so on). Beyond this, the growth is exponential; speeds much higher than the exhaust velocity require very high ratios of fuel mass to payload and structural mass.

For a mission, for example, when launching from or landing on a planet, the effects of gravitational attraction and any atmospheric drag must be overcome by using fuel. It is typical to combine the effects of these and other effects into an effective mission delta-v. For example, a launch mission to low Earth orbit requires about 9.3–10 km/s delta-v. These mission delta-vs are typically numerically integrated on a computer.

Some effects such as Oberth effect can only be significantly utilised by high thrust engines such as rockets; i.e., engines that can produce a high g-force (thrust per unit mass, equal to delta-v per unit time).

Energy

In the ideal case ${\displaystyle m_{1}}$ is useful payload and ${\displaystyle m_{0}-m_{1}}$ is reaction mass (this corresponds to empty tanks having no mass, etc.). The energy required can simply be computed as

${\displaystyle {\frac {1}{2}}(m_{0}-m_{1})v_{\text{e}}^{2}}$

This corresponds to the kinetic energy the expelled reaction mass would have at a speed equal to the exhaust speed. If the reaction mass had to be accelerated from zero speed to the exhaust speed, all energy produced would go into the reaction mass and nothing would be left for kinetic energy gain by the rocket and payload. However, if the rocket already moves and accelerates (the reaction mass is expelled in the direction opposite to the direction in which the rocket moves) less kinetic energy is added to the reaction mass. To see this, if, for example, ${\displaystyle v_{e}}$=10 km/s and the speed of the rocket is 3 km/s, then the speed of a small amount of expended reaction mass changes from 3 km/s forwards to 7 km/s rearwards. Thus, although the energy required is 50 MJ per kg reaction mass, only 20 MJ is used for the increase in speed of the reaction mass. The remaining 30 MJ is the increase of the kinetic energy of the rocket and payload.

In general:

${\displaystyle d\left({\frac {1}{2}}v^{2}\right)=vdv=vv_{\text{e}}{\frac {dm}{m}}={\frac {1}{2}}\left{\frac {dm}{m}}}$

Thus the specific energy gain of the rocket in any small time interval is the energy gain of the rocket including the remaining fuel, divided by its mass, where the energy gain is equal to the energy produced by the fuel minus the energy gain of the reaction mass. The larger the speed of the rocket, the smaller the energy gain of the reaction mass; if the rocket speed is more than half of the exhaust speed the reaction mass even loses energy on being expelled, to the benefit of the energy gain of the rocket; the larger the speed of the rocket, the larger the energy loss of the reaction mass.

We have

${\displaystyle \Delta \epsilon =\int v\,d(\Delta v)}$

where ${\displaystyle \epsilon }$ is the specific energy of the rocket (potential plus kinetic energy) and ${\displaystyle \Delta v}$Zdroj:https://en.wikipedia.org?pojem=Reaction_engine
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.