In set theory, the Schröder–Bernstein theorem states that, if there exist injective functions f : A → B and g : B → A between the sets A and B, then there exists a bijective function h : A → B.

In terms of the cardinality of the two sets, this classically implies that if |A| ≤ |B| and |B| ≤ |A|, then |A| = |B|; that is, A and B are equipotent. This is a useful feature in the ordering of cardinal numbers.

The theorem is named after Felix Bernstein and Ernst Schröder. It is also known as the Cantor–Bernstein theorem or Cantor–Schröder–Bernstein theorem, after Georg Cantor, who first published it (albeit without proof).

Proof

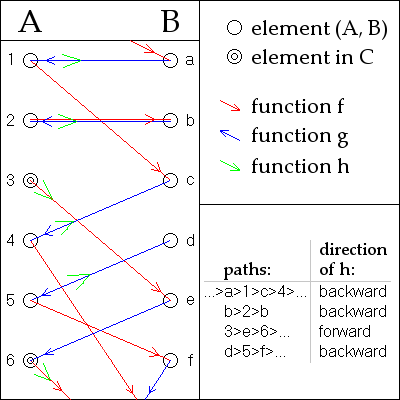
The following proof is attributed to Julius König.^[1]

Assume without loss of generality that A and B are disjoint. For any a in A or b in B we can form a unique two-sided sequence of elements that are alternately in A and B, by repeatedly applying ${\displaystyle f}$ and ${\displaystyle g^{-1}}$ to go from A to B and ${\displaystyle g}$ and ${\displaystyle f^{-1}}$ to go from B to A (where defined; the inverses ${\displaystyle f^{-1}}$ and ${\displaystyle g^{-1}}$ are understood as partial functions.)

${\displaystyle \cdots \rightarrow f^{-1}(g^{-1}(a))\rightarrow g^{-1}(a)\rightarrow a\rightarrow f(a)\rightarrow g(f(a))\rightarrow \cdots }$

For any particular a, this sequence may terminate to the left or not, at a point where ${\displaystyle f^{-1}}$ or ${\displaystyle g^{-1}}$ is not defined.

By the fact that ${\displaystyle f}$ and ${\displaystyle g}$ are injective functions, each a in A and b in B is in exactly one such sequence to within identity: if an element occurs in two sequences, all elements to the left and to the right must be the same in both, by the definition of the sequences. Therefore, the sequences form a partition of the (disjoint) union of A and B. Hence it suffices to produce a bijection between the elements of A and B in each of the sequences separately, as follows:

Call a sequence an A-stopper if it stops at an element of A, or a B-stopper if it stops at an element of B. Otherwise, call it doubly infinite if all the elements are distinct or cyclic if it repeats. See the picture for examples.

• For an A-stopper, the function ${\displaystyle f}$ is a bijection between its elements in A and its elements in B.
• For a B-stopper, the function ${\displaystyle g}$ is a bijection between its elements in B and its elements in A.
• For a doubly infinite sequence or a cyclic sequence, either ${\displaystyle f}$ or ${\displaystyle g}$ will do (${\displaystyle g}$ is used in the picture).

Examples

Bijective function from ${\displaystyle 0,1\to 0,1)}$

Note: ${\displaystyle 0,1)}$ is the half open set from 0 to 1, including the boundary 0 and excluding the boundary 1.

Let ${\displaystyle f:0,1\to 0,1)\;}$ with ${\displaystyle f(x)=x/2;\;}$ and ${\displaystyle g:0,1)\to 0,1\;}$ with ${\displaystyle g(x)=x;\;}$ the two injective functions.

In line with that procedure ${\displaystyle C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}}$

Then ${\displaystyle \;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in 0,1\setminus C\end{cases}}\;}$ is a bijective function from ${\displaystyle 0,1\to 0,1)}$.

Bijective function from ${\displaystyle 0,2)\to 0,1)^{2}}$

Let ${\displaystyle f:0,2)\to 0,1)^{2}\;}$ with ${\displaystyle f(x)=(x/2;0);\;}$

Then for ${\displaystyle (x;y)\in 0,1)^{2}\;}$ one can use the expansions ${\displaystyle \;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;}$ and ${\displaystyle \;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;}$ with ${\displaystyle \;a_{k},b_{k}\in \{0,1,...,9\}\;}$

and now one can set $$Zdroj:https://en.wikipedia.org?pojem=Schröder–Bernstein_theorem
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---