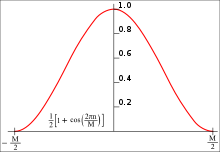
In signal processing and statistics, a window function (also known as an apodization function or tapering function^[1]) is a mathematical function that is zero-valued outside of some chosen interval. Typically, window functions are symmetric around the middle of the interval, approach a maximum in the middle, and taper away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions.

The reasons for examining segments of a longer function include detection of transient events and time-averaging of frequency spectra. The duration of the segments is determined in each application by requirements like time and frequency resolution. But that method also changes the frequency content of the signal by an effect called spectral leakage. Window functions allow us to distribute the leakage spectrally in different ways, according to the needs of the particular application. There are many choices detailed in this article, but many of the differences are so subtle as to be insignificant in practice.

In typical applications, the window functions used are non-negative, smooth, "bell-shaped" curves.^[2] Rectangle, triangle, and other functions can also be used. A more general definition of window functions does not require them to be identically zero outside an interval, as long as the product of the window multiplied by its argument is square integrable, and, more specifically, that the function goes sufficiently rapidly toward zero.^[3]

Applications

Window functions are used in spectral analysis/modification/resynthesis,^[4] the design of finite impulse response filters, merging multiscale and multidimensional datasets,^[5][6] as well as beamforming and antenna design.

Spectral analysis

The Fourier transform of the function cos(ωt) is zero, except at frequency ±ω. However, many other functions and waveforms do not have convenient closed-form transforms. Alternatively, one might be interested in their spectral content only during a certain time period.

In either case, the Fourier transform (or a similar transform) can be applied on one or more finite intervals of the waveform. In general, the transform is applied to the product of the waveform and a window function. Any window (including rectangular) affects the spectral estimate computed by this method.

Filter design

Windows are sometimes used in the design of digital filters, in particular to convert an "ideal" impulse response of infinite duration, such as a sinc function, to a finite impulse response (FIR) filter design. That is called the window method.^[7][8][9]

Statistics and curve fitting

Window functions are sometimes used in the field of statistical analysis to restrict the set of data being analyzed to a range near a given point, with a weighting factor that diminishes the effect of points farther away from the portion of the curve being fit. In the field of Bayesian analysis and curve fitting, this is often referred to as the kernel.

Rectangular window applications

Analysis of transients

When analyzing a transient signal in modal analysis, such as an impulse, a shock response, a sine burst, a chirp burst, or noise burst, where the energy vs time distribution is extremely uneven, the rectangular window may be most appropriate. For instance, when most of the energy is located at the beginning of the recording, a non-rectangular window attenuates most of the energy, degrading the signal-to-noise ratio.^[10]

Harmonic analysis

One might wish to measure the harmonic content of a musical note from a particular instrument or the harmonic distortion of an amplifier at a given frequency. Referring again to Figure 2, we can observe that there is no leakage at a discrete set of harmonically-related frequencies sampled by the discrete Fourier transform (DFT). (The spectral nulls are actually zero-crossings, which cannot be shown on a logarithmic scale such as this.) This property is unique to the rectangular window, and it must be appropriately configured for the signal frequency, as described above.

Overlapping windows

When the length of a data set to be transformed is larger than necessary to provide the desired frequency resolution, a common practice is to subdivide it into smaller sets and window them individually. To mitigate the "loss" at the edges of the window, the individual sets may overlap in time. See Welch method of power spectral analysis and the modified discrete cosine transform.

Two-dimensional windows

Two-dimensional windows are commonly used in image processing to reduce unwanted high-frequencies in the image Fourier transform.^[11] They can be constructed from one-dimensional windows in either of two forms.^[12] The separable form, ${\displaystyle W(m,n)=w(m)w(n)}$ is trivial to compute. The radial form, ${\displaystyle W(m,n)=w(r)}$, which involves the radius ${\displaystyle r={\sqrt {(m-M/2)^{2}+(n-N/2)^{2}}}}$, is isotropic, independent on the orientation of the coordinate axes. Only the Gaussian function is both separable and isotropic.^[13] The separable forms of all other window functions have corners that depend on the choice of the coordinate axes. The isotropy/anisotropy of a two-dimensional window function is shared by its two-dimensional Fourier transform. The difference between the separable and radial forms is akin to the result of diffraction from rectangular vs. circular apertures, which can be visualized in terms of the product of two sinc functions vs. an Airy function, respectively.

Examples of window functions

Conventions:

• ${\displaystyle w_{0}(x)}$ is a zero-phase function (symmetrical about ${\displaystyle x=0}$),^[14] continuous for ${\displaystyle x\in ,}$ where ${\displaystyle N}$ is a positive integer (even or odd).^[15]
• The sequence ${\displaystyle \{w=w_0(n-<!--\; -\; -->N/2),0}$Zdroj:https://en.wikipedia.org?pojem=Tukey_window
  Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

  ---