Average

In ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean – the sum of the numbers divided by how many numbers are in the list. For example, the mean average of the numbers 2, 3, 4, 7, and 9 (summing to 25) is 5. Depending on the context, the most representative statistic to be taken as the average might be another measure of central tendency, such as the mid-range, median, mode or geometric mean. For example, the average personal income is often given as the median – the number below which are 50% of personal incomes and above which are 50% of personal incomes – because the mean would be higher by including personal incomes from a few billionaires. For this reason, it is recommended to avoid using the word "average" when discussing measures of central tendency and specify which type of measure of average is being used.

General properties

If all numbers in a list are the same number, then their average is also equal to this number. This property is shared by each of the many types of average.

Another universal property is monotonicity: if two lists of numbers A and B have the same length, and each entry of list A is at least as large as the corresponding entry on list B, then the average of list A is at least that of list B. Also, all averages satisfy linear homogeneity: if all numbers of a list are multiplied by the same positive number, then its average changes by the same factor.

In some types of average, the items in the list are assigned different weights before the average is determined. These include the weighted arithmetic mean, the weighted geometric mean and the weighted median. Also, for some types of moving average, the weight of an item depends on its position in the list. Most types of average, however, satisfy permutation-insensitivity: all items count equally in determining their average value and their positions in the list are irrelevant; the average of (1, 2, 3, 4, 6) is the same as that of (3, 2, 6, 4, 1).

Pythagorean means

The arithmetic mean, the geometric mean and the harmonic mean are known collectively as the Pythagorean means.

Statistical location

The mode, the median, and the mid-range are often used in addition to the mean as estimates of central tendency in descriptive statistics. These can all be seen as minimizing variation by some measure; see Central tendency § Solutions to variational problems.

Comparison of common averages of values { 1, 2, 2, 3, 4, 7, 9 }
Type	Description	Example	Result
Arithmetic mean	Sum of values of a data set divided by number of values: $\scriptstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$	(1+2+2+3+4+7+9) / 7	4
Median	Middle value separating the greater and lesser halves of a data set	1, 2, 2, 3, 4, 7, 9	3
Mode	Most frequent value in a data set	1, 2, 2, 3, 4, 7, 9	2
Mid-range	The arithmetic mean of the highest and lowest values of a set	(1+9) / 2	5

Mode

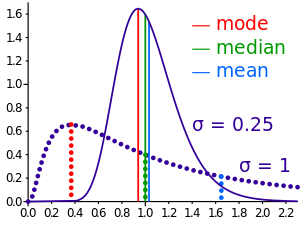
The most frequently occurring number in a list is called the mode. For example, the mode of the list (1, 2, 2, 3, 3, 3, 4) is 3. It may happen that there are two or more numbers which occur equally often and more often than any other number. In this case there is no agreed definition of mode. Some authors say they are all modes and some say there is no mode.

Median

The median is the middle number of the group when they are ranked in order. (If there are an even number of numbers, the mean of the middle two is taken.)

Thus to find the median, order the list according to its elements' magnitude and then repeatedly remove the pair consisting of the highest and lowest values until either one or two values are left. If exactly one value is left, it is the median; if two values, the median is the arithmetic mean of these two. This method takes the list 1, 7, 3, 13 and orders it to read 1, 3, 7, 13. Then the 1 and 13 are removed to obtain the list 3, 7. Since there are two elements in this remaining list, the median is their arithmetic mean, (3 + 7)/2 = 5.

Mid-range

The mid-range is the arithmetic mean of the highest and lowest values of a set.

Summary of types

Name	Equation or description	As solution to optimization problem
Arithmetic mean	${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n})$	${\underset {x\in \mathbb {R} }{\operatorname {argmin} }}\,\sum _{i=1}^{n}(x-x_{i})^{2}$
Median	A middle value that separates the higher half from the lower half of the data set; may not be unique if the data set contains an even number of points	${\underset {x\in \mathbb {R} }{\operatorname {argmin} }}\,\sum _{i=1}^{n}\|x-x_{i}\|$
Geometric median	A rotation invariant extension of the median for points in $\mathbb {R} ^{d}$	${\underset {{\vec {x}}\in \mathbb {R} ^{d}}{\operatorname {argmin} }}\,\sum _{i=1}^{n}\|\|{\vec {x}}-{\vec {x}}_{i}\|\|_{2}$
Tukey median	Another rotation invariant extension of the median for points in $\mathbb {R} ^{d}$ —a point that maximizes the Tukey depth	${\underset {{\vec {x}}\in \mathbb {R} ^{d}}{\operatorname {argmax} }}\,{\underset {{\vec {u}}\in \mathbb {R} ^{d}}{\operatorname {min} }}\,\sum _{i=1}^{n}\left({\begin{cases}1,{\text{ if }}({\vec {x}}_{i}-{\vec {x}})\cdot {\vec {u}}\geq 0\\0,{\text{ otherwise}}\end{cases}}\right)$
Mode	The most frequent value in the data set	${\underset {x\in \mathbb {R} }{\operatorname {argmax} }}\,\sum _{i=1}^{n}\left({\begin{cases}1,{\text{ if }}x=x_{i}\\0,{\text{ if }}x\neq x_{i}\end{cases}}\right)$
Geometric mean	${\sqrt{\prod _{i=1}^{n}x_{i}}}={\sqrt{x_{1}\cdot x_{2}\dotsb x_{n}}}$