Part of a series on
Numeral systems
Place-value notation Hindu–Arabic numerals Western Arabic Eastern Arabic Bengali Devanagari Gujarati Gurmukhi Odia Sinhala Tamil Malayalam Telugu Kannada Dzongkha Tibetan Balinese Burmese Javanese Khmer Lao Mongolian Sundanese Thai East Asian systems Contemporary Chinese Suzhou Hokkien Japanese Korean Vietnamese Historic Counting rods Tangut Other systems History Ancient Babylonian Post-classical Cistercian Mayan Muisca Pentadic Quipu Rumi Contemporary Cherokee Kaktovik (Iñupiaq) By radix/base Common radices/bases 2 3 4 5 6 8 10 12 16 20 60 (table) Non-standard radices/bases Bijective (1) Signed-digit (balanced ternary) Mixed (factorial) Negative Complex (2i) Non-integer (φ) Asymmetric
Sign-value notation Non-alphabetic Aegean Attic Aztec Brahmi Chuvash Egyptian Etruscan Kharosthi Prehistoric counting Proto-cuneiform Roman Tally marks Alphabetic Abjad Armenian Alphasyllabic Akṣarapallī Āryabhaṭa Kaṭapayādi Coptic Cyrillic Geʽez Georgian Glagolitic Greek Hebrew
List of numeral systems
v t e

A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method for represening numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A binary number may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two.

The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation.^[1]

History

The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, Juan Caramuel y Lobkowitz, and Gottfried Leibniz. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India.

Egypt

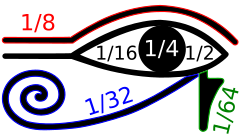
The scribes of ancient Egypt used two different systems for their fractions, Egyptian fractions (not related to the binary number system) and Horus-Eye fractions (so called because many historians of mathematics believe that the symbols used for this system could be arranged to form the eye of Horus, although this has been disputed).^[2] Horus-Eye fractions are a binary numbering system for fractional quantities of grain, liquids, or other measures, in which a fraction of a hekat is expressed as a sum of the binary fractions 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64. Early forms of this system can be found in documents from the Fifth Dynasty of Egypt, approximately 2400 BC, and its fully developed hieroglyphic form dates to the Nineteenth Dynasty of Egypt, approximately 1200 BC.^[3]

The method used for ancient Egyptian multiplication is also closely related to binary numbers. In this method, multiplying one number by a second is performed by a sequence of steps in which a value (initially the first of the two numbers) is either doubled or has the first number added back into it; the order in which these steps are to be performed is given by the binary representation of the second number. This method can be seen in use, for instance, in the Rhind Mathematical Papyrus, which dates to around 1650 BC.^[4]

China

The I Ching dates from the 9th century BC in China.^[5] The binary notation in the I Ching is used to interpret its quaternary divination technique.^[6]

It is based on taoistic duality of yin and yang.^[7] Eight trigrams (Bagua) and a set of 64 hexagrams ("sixty-four" gua), analogous to the three-bit and six-bit binary numerals, were in use at least as early as the Zhou Dynasty of ancient China.^[5]

The Song Dynasty scholar Shao Yong (1011–1077) rearranged the hexagrams in a format that resembles modern binary numbers, although he did not intend his arrangement to be used mathematically.^[6] Viewing the least significant bit on top of single hexagrams in Shao Yong's square^[8] and reading along rows either from bottom right to top left with solid lines as 0 and broken lines as 1 or from top left to bottom right with solid lines as 1 and broken lines as 0 hexagrams can be interpreted as sequence from 0 to 63. ^[9]

India

The Indian scholar Pingala (c. 2nd century BC) developed a binary system for describing prosody.^[10][11] He described meters in the form of short and long syllables (the latter equal in length to two short syllables).^[12] They were known as laghu (light) and guru (heavy) syllables.

Pingala's Hindu classic titled Chandaḥśāstra (8.23) describes the formation of a matrix in order to give a unique value to each meter. "Chandaḥśāstra" literally translates to science of meters in Sanskrit. The binary representations in Pingala's system increases towards the right, and not to the left like in the binary numbers of the modern positional notation.^[13] In Pingala's system, the numbers start from number one, and not zero. Four short syllables "0000" is the first pattern and corresponds to the value one. The numerical value is obtained by adding one to the sum of place values.^[14]

Other cultures

The residents of the island of Mangareva in French Polynesia were using a hybrid binary-decimal system before 1450.^[15] Slit drums with binary tones are used to encode messages across Africa and Asia.^[7] Sets of binary combinations similar to the I Ching have also been used in traditional African divination systems such as Ifá as well as in medieval Western geomancy. The majority of Indigenous Australian languages use a base-2 system.^[16]

Western predecessors to Leibniz

In the late 13th century Ramon Llull had the ambition to account for all wisdom in every branch of human knowledge of the time. For that purpose he developed a general method or "Ars generalis" based on binary combinations of a number of simple basic principles or categories, for which he has been considered a predecessor of computing science and artificial intelligence.^[17]

In 1605, Francis Bacon discussed a system whereby letters of the alphabet could be reduced to sequences of binary digits, which could then be encoded as scarcely visible variations in the font in any random text.^[18] Importantly for the general theory of binary encoding, he added that this method could be used with any objects at all: "provided those objects be capable of a twofold difference only; as by Bells, by Trumpets, by Lights and Torches, by the report of Muskets, and any instruments of like nature".^[18] (See Bacon's cipher.)

In 1617, John Napier described a system he called location arithmetic for doing binary calculations using a non-positional representation by letters. Thomas Harriot investigated several positional numbering systems, including binary, but did not publish his results; they were found later among his papers.^[19] Possibly the first publication of the system in Europe was by Juan Caramuel y Lobkowitz, in 1700.^[20]

Leibniz and the I Ching

Leibniz studied binary numbering in 1679; his work appears in his article Explication de l'Arithmétique Binaire (published in 1703). The full title of Leibniz's article is translated into English as the "Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi".^[21] Leibniz's system uses 0 and 1, like the modern binary numeral system. An example of Leibniz's binary numeral system is as follows:^[21]

0 0 0 1   numerical value 2⁰

0 0 1 0   numerical value 2¹

0 1 0 0   numerical value 2²

1 0 0 0   numerical value 2³

While corresponding with the Jesuit priest Joachim Bouvet in 1700, who had made himself an expert on the I Ching while a missionary in China, Leibniz explained his binary notation, and Bouvet demonstrated in his 1701 letters that the I Ching was an independent, parallel invention of binary notation. Leibniz & Bouvet concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical mathematics he admired.^[22] Of this parallel invention, Liebniz wrote in his "Explanation Of Binary Arithmetic" that "this restitution of their meaning, after such a great interval of time, will seem all the more curious."^[23]

The relation was a central idea to his universal concept of a language or characteristica universalis, a popular idea that would be followed closely by his successors such as Gottlob Frege and George Boole in forming modern symbolic logic.^[24] Leibniz was first introduced to the I Ching through his contact with the French Jesuit Joachim Bouvet, who visited China in 1685 as a missionary. Leibniz saw the I Ching hexagrams as an affirmation of the universality of his own religious beliefs as a Christian.^[25] Binary numerals were central to Leibniz's theology. He believed that binary numbers were symbolic of the Christian idea of creatio ex nihilo or creation out of nothing.^[26]

is not easy to impart to the pagans, is the creation ex nihilo through God's almighty power. Now one can say that nothing in the world can better present and demonstrate this power than the origin of numbers, as it is presented here through the simple and unadorned presentation of One and Zero or Nothing.

— Leibniz's letter to the Duke of Brunswick attached with the I Ching hexagrams^[25]

Later developments

In 1854, British mathematician George Boole published a landmark paper detailing an algebraic system of logic that would become known as Boolean algebra. His logical calculus was to become instrumental in the design of digital electronic circuitry.^[27]

In 1937, Claude Shannon produced his master's thesis at MIT that implemented Boolean algebra and binary arithmetic using electronic relays and switches for the first time in history. Entitled A Symbolic Analysis of Relay and Switching Circuits, Shannon's thesis essentially founded practical digital circuit design.^[28]

In November 1937, George Stibitz, then working at Bell Labs, completed a relay-based computer he dubbed the "Model K" (for "Kitchen", where he had assembled it), which calculated using binary addition.^[29] Bell Labs authorized a full research program in late 1938 with Stibitz at the helm. Their Complex Number Computer, completed 8 January 1940, was able to calculate complex numbers. In a demonstration to the American Mathematical Society conference at Dartmouth College on 11 September 1940, Stibitz was able to send the Complex Number Calculator remote commands over telephone lines by a teletype. It was the first computing machine ever used remotely over a phone line. Some participants of the conference who witnessed the demonstration were John von Neumann, John Mauchly and Norbert Wiener, who wrote about it in his memoirs.^[30][31][32]

The Z1 computer, which was designed and built by Konrad Zuse between 1935 and 1938, used Boolean logic and binary floating-point numbers.^[33]

Representation

Any number can be represented by a sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Any of the following rows of symbols can be interpreted as the binary numeric value of 667:

1	0	1	0	0	1	1	0	1	1
|	―	|	―	―	|	|	―	|	|
☒	☐	☒	☐	☐	☒	☒	☐	☒	☒
y	n	y	n	n	y	y	n	y	y

The numeric value represented in each case depends on the value assigned to each symbol. In the earlier days of computing, switches, punched holes, and punched paper tapes were used to represent binary values.^[34] In a modern computer, the numeric values may be represented by two different voltages; on a magnetic disk, magnetic polarities may be used. A "positive", "yes", or "on" state is not necessarily equivalent to the numerical value of one; it depends on the architecture in use.

In keeping with the customary representation of numerals using Arabic numerals, binary numbers are commonly written using the symbols 0 and 1. When written, binary numerals are often subscripted, prefixed, or suffixed to indicate their base, or radix. The following notations are equivalent:

• 100101 binary (explicit statement of format)
• 100101b (a suffix indicating binary format; also known as Intel convention^[35][36])
• 100101B (a suffix indicating binary format)
• bin 100101 (a prefix indicating binary format)
• 100101₂ (a subscript indicating base-2 (binary) notation)
• %100101 (a prefix indicating binary format; also known as Motorola convention^[35][36])
• 0b100101 (a prefix indicating binary format, common in programming languages)
• 6b100101 (a prefix indicating number of bits in binary format, common in programming languages)
• #b100101 (a prefix indicating binary format, common in Lisp programming languages)

When spoken, binary numerals are usually read digit-by-digit, to distinguish them from decimal numerals. For example, the binary numeral 100 is pronounced one zero zero, rather than one hundred, to make its binary nature explicit and for purposes of correctness. Since the binary numeral 100 represents the value four, it would be confusing to refer to the numeral as one hundred (a word that represents a completely different value, or amount). Alternatively, the binary numeral 100 can be read out as "four" (the correct value), but this does not make its binary nature explicit.

Counting in binary

Decimal number	Binary number
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111

Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. Before examining binary counting, it is useful to briefly discuss the more familiar decimal counting system as a frame of reference.

Decimal counting

Decimal counting uses the ten symbols 0 through 9. Counting begins with the incremental substitution of the least significant digit (rightmost digit) which is often called the first digit. When the available symbols for this position are exhausted, the least significant digit is reset to 0, and the next digit of higher significance (one position to the left) is incremented (overflow), and incremental substitution of the low-order digit resumes. This method of reset and overflow is repeated for each digit of significance. Counting progresses as follows:

000, 001, 002, ... 007, 008, 009, (rightmost digit is reset to zero, and the digit to its left is incremented)

010, 011, 012, ...

   ...

090, 091, 092, ... 097, 098, 099, (rightmost two digits are reset to zeroes, and next digit is incremented)

100, 101, 102, ...

Binary counting

Binary counting follows the exact same procedure, and again the incremental substitution begins with the least significant binary digit, or bit (the rightmost one, also called the first bit), except that only the two symbols 0 and 1 are available. Thus, after a bit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next bit to the left:

0000,

0001, (rightmost bit starts over, and the next bit is incremented)

0010, 0011, (rightmost two bits start over, and the next bit is incremented)

0100, 0101, 0110, 0111, (rightmost three bits start over, and the next bit is incremented)

1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...

In the binary system, each bit represents an increasing power of 2, with the rightmost bit representing 2⁰, the next representing 2¹, then 2², and so on. The value of a binary number is the sum of the powers of 2 represented by each "1" bit. For example, the binary number 100101 is converted to decimal form as follows:

100101₂ = + + + + +

100101₂ = + + + + 0 × 2 + 1 × 1

100101₂ = 37₁₀

Fractionsedit

Fractions in binary arithmetic terminate only if 2 is the only prime factor in the denominator. As a result, 1/10 does not have a finite binary representation (10 has prime factors 2 and 5). This causes 10 × 1/10 not to precisely equal 1 in binary floating-point arithmetic. As an example, to interpret the binary expression for 1/3 = .010101..., this means: 1/3 = 0 × 2⁻¹ + 1 × 2⁻² + 0 × 2⁻³ + 1 × 2⁻⁴ + ... = 0.3125 + ... An exact value cannot be found with a sum of a finite number of inverse powers of two, the zeros and ones in the binary representation of 1/3 alternate forever.

Fraction	Decimal	Binary	Fractional approximation
1/1	1 or 0.999...	1 or 0.111...	1/2 + 1/4 + 1/8...
1/2	0.5 or 0.4999...	0.1 or 0.0111...	1/4 + 1/8 + 1/16 . . .
1/3	0.333...	0.010101...	1/4 + 1/16 + 1/64 . . .
1/4	0.25 or 0.24999...	0.01 or 0.00111...	1/8 + 1/16 + 1/32 . . .
1/5	0.2 or 0.1999...	0.00110011...	1/8 + 1/16 + 1/128 . . .
1/6	0.1666...	0.0010101...	1/8 + 1/32 + 1/128 . . .
1/7	0.142857142857...	0.001001...	1/8 + 1/64 + 1/512 . . .
1/8	0.125 or 0.124999...	0.001 or 0.000111...	1/16 + 1/32 + 1/64 . . .
1/9	0.111...	0.000111000111...	1/16 + 1/32 + 1/64 . . .
1/10	0.1 or 0.0999...	0.000110011...	1/16 + 1/32 + 1/256 . . .
1/11	0.090909...	0.00010111010001011101...	1/16 + 1/64 + 1/128 . . .
1/12	0.08333...	0.00010101...	1/16 + 1/64 + 1/256 . . .
1/13	0.076923076923...	0.000100111011000100111011...	1/16 + 1/128 + 1/256 . . .
1/14	0.0714285714285...	0.0001001001...	1/16 + 1/128 + 1/1024 . . .
1/15	0.0666...	0.00010001...	1/16 + 1/256 . . .
1/16	0.0625 or 0.0624999...	0.0001 or 0.0000111...	1/32 + 1/64 + 1/128 . . .

Binary arithmeticedit

Arithmetic in binary is much like arithmetic in other positional notation numeral systems. Addition, subtraction, multiplication, and division can be performed on binary numerals.

Additionedit

The simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple, using a form of carrying:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 2¹) )

Adding two "1" digits produces a digit "0", while 1 will have to be added to the next column. This is similar to what happens in decimal when certain single-digit numbers are added together; if the result equals or exceeds the value of the radix (10), the digit to the left is incremented:

5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 10¹) )

7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 10¹) )

This is known as carrying. When the result of an addition exceeds the value of a digit, the procedure is to "carry" the excess amount divided by the radix (that is, 10/10) to the left, adding it to the next positional value. This is correct since the next position has a weight that is higher by a factor equal to the radix. Carrying works the same way in binary:

  1 1 1 1 1    (carried digits)
    0 1 1 0 1
+   1 0 1 1 1
-------------
= 1 0 0 1 0 0 = 36

In this example, two numerals are being added together: 01101₂ (13₁₀) and 10111₂ (23₁₀). The top row shows the carry bits used. Starting in the rightmost column, 1 + 1 = 10₂. The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added: 1 + 0 + 1 = 10₂ again; the 1 is carried, and 0 is written at the bottom. The third column: 1 + 1 + 1 = 11₂. This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 100100₂ (36₁₀).

When computers must add two numbers, the rule that: x xor y = (x + y) mod 2 for any two bits x and y allows for very fast calculation, as well.

Zdroj:https://en.wikipedia.org?pojem=Binary_arithmetic
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---