The Duckworth–Lewis–Stern method (DLS) is a mathematical formulation designed to calculate the target score (number of runs needed to win) for the team batting second in a limited overs cricket match interrupted by weather or other circumstances. The method was devised by two English statisticians, Frank Duckworth and Tony Lewis, and was formerly known as the Duckworth–Lewis method (D/L).^[1] It was introduced in 1997, and adopted officially by the ICC in 1999. After the retirement of both Duckworth and Lewis, the Australian statistician Steven Stern became the custodian of the method, which was renamed to its current title in November 2014.^[2][3] In 2014, he refined the model to better fit modern scoring trends, especially in T20 cricket, resulting in the updated Duckworth-Lewis-Stern method.^[4] This refined method remains the standard for handling rain-affected matches in international cricket today.

The target score in cricket matches without interruptions is one more than the number of runs scored by the team that batted first. When overs are lost, setting an adjusted target for the team batting second is not as simple as reducing the run target proportionally to the loss in overs, because a team with ten wickets in hand and 25 overs to bat can play more aggressively than if they had ten wickets and a full 50 overs, for example, and can consequently achieve a higher run rate. The DLS method is an attempt to set a statistically fair target for the second team's innings, which is the same difficulty as the original target. The basic principle is that each team in a limited-overs match has two resources available with which to score runs (overs to play and wickets remaining), and the target is adjusted proportionally to the change in the combination of these two resources.

History and creation

Various different methods had been used previously to resolve rain-affected cricket matches, with the most common being the Average Run Rate method, and later, the Most Productive Overs method.

While simple in nature, these methods had intrinsic flaws and were easily exploitable:

• The Average Run Rate method took no account of wickets lost by the team batting second, but simply reflected their scoring rate when the match was interrupted. If the team felt a rain stoppage was likely, they could attempt to force the scoring rate with no regard for the corresponding highly likely loss of wickets, meaning any comparison with the team batting first would be flawed.
• The Most Productive Overs method not only took no account of wickets lost by the team batting second, but also effectively penalised the team batting second for good bowling by ignoring their best overs in setting the revised target.
• Both of these methods also produced revised targets that frequently altered the balance of the match, and they took no account of the match situation at the time of the interruption.

The D/L method was devised by two British statisticians, Frank Duckworth and Tony Lewis, as a result of the outcome of the semi-final in the 1992 World Cup between England and South Africa, where the Most Productive Overs method was used.

When rain stopped play for 12 minutes, South Africa needed 22 runs from 13 balls, but when play resumed, the revised target left South Africa needing 21 runs from one ball, a reduction of only one run compared to a reduction of two overs, and a virtually impossible target given that the maximum score from one ball is generally six runs.^[5]

Duckworth said, "I recall hearing Christopher Martin-Jenkins on radio saying 'surely someone, somewhere could come up with something better' and I soon realised that it was a mathematical problem that required a mathematical solution."^[6][7]

The D/L method avoids this flaw: in this match, the revised D/L target of 236 would have left South Africa needing four to tie or five to win from the final ball.^{[8][nb 1]}

The D/L method was first used in international cricket on 1 January 1997 in the second match of the Zimbabwe versus England ODI series, which Zimbabwe won by seven runs.^[11] The D/L method was formally adopted by the ICC in 1999 as the standard method of calculating target scores in rain-shortened one-day matches.

Theory

Calculation summary

The essence of the D/L method is 'resources'. Each team is taken to have two 'resources' to use to score as many runs as possible: the number of overs they have to receive; and the number of wickets they have in hand. At any point in any innings, a team's ability to score more runs depends on the combination of these two resources they have left. Looking at historical scores, there is a very close correspondence between the availability of these resources and a team's final score, a correspondence which D/L exploits.^[12]

The D/L method converts all possible combinations of overs (or, more accurately, balls) and wickets left into a combined resources remaining percentage figure (with 50 overs and 10 wickets = 100%), and these are all stored in a published table or computer. The target score for the team batting second ('Team 2') can be adjusted up or down from the total the team batting first ('Team 1') achieved using these resource percentages, to reflect the loss of resources to one or both teams when a match is shortened one or more times.

In the version of D/L most commonly in use in international and first-class matches (the 'Professional Edition'), the target for Team 2 is adjusted simply in proportion to the two teams' resources, i.e.

${\displaystyle {\text{Team 2's par score }}={\text{ Team 1's score}}\times {\frac {\text{Team 2's resources}}{\text{Team 1's resources}}}.}$

If, as usually occurs, this 'par score' is a non-integer number of runs, then Team 2's target to win is this number rounded up to the next integer, and the score to tie (also called the par score), is this number rounded down to the preceding integer. If Team 2 reaches or passes the target score, then they have won the match. If the match ends when Team 2 has exactly met (but not passed) the par score then the match is a tie. If Team 2 fail to reach the par score then they have lost.

For example, if a rain delay means that Team 2 only has 90% of resources available, and Team 1 scored 254 with 100% of resources available, then 254 × 90% / 100% = 228.6, so Team 2's target is 229, and the score to tie is 228. The actual resource values used in the Professional Edition are not publicly available,^[13] so a computer which has this software loaded must be used.

If it is a 50-over match and Team 1 completed its innings uninterrupted, then they had 100% resource available to them, so the formula simplifies to:

${\displaystyle {\text{Team 2's par score }}={\text{ Team 1's score}}\times {\text{Team 2's resources}}.}$

Summary of impact on Team 2's target

• If there is a delay before the first innings starts, so that the numbers of overs in the two innings are reduced but still the same as each other, then D/L makes no change to the target score, because both sides are aware of the total number of overs and wickets throughout their innings, thus they will have the same resources available.
• Team 2's target score is first calculated once Team 1's innings has finished.
• If there were interruption(s) during Team 1's innings, or Team 1's innings was cut short, so the numbers of overs in the two innings are reduced (but still the same as each other), then D/L will adjust Team 2's target score as described above. The adjustment to Team 2's target after interruptions in Team 1's innings is often an increase, implying that Team 2 has more resource available than Team 1 had. Although both teams have 10 wickets and the same (reduced) number of overs available, an increase is fair as, for some of their innings, Team 1 thought they would have more overs available than they actually ended up having. If Team 1 had known that their innings was going to be shorter, they would have batted less conservatively, and scored more runs (at the expense of more wickets). They saved some wicket resource to use up in the overs that ended up being cancelled, which Team 2 does not need to do, therefore Team 2 does have more resource to use in the same number of overs. Therefore, increasing Team 2's target score compensates Team 1 for the denial of some of the overs they thought they would get to bat. The increased target is what D/L thinks Team 1 would have scored in the overs it ended up having, if it had known throughout that the innings would be only as long as it was.

For example, if Team 1 batted for 20 overs before rain came, thinking they would have 50 overs in total, but at the re-start there was only time for Team 2 to bat for 20 overs, it would clearly be unfair to give Team 2 the target that Team 1 achieved, as Team 1 would have batted less conservatively and scored more runs, if they had known they would only have the 20 overs.

• If there are interruption(s) to Team 2's innings, either before it starts, during, or it is cut short, then D/L will reduce Team 2's target score from the initial target set at the end of Team 1's innings, in proportion to the reduction in Team 2's resources. If there are multiple interruptions in the second innings, the target will be adjusted downwards each time.
• If there are interruptions which both increase and decrease the target score, then the net effect on the target could be either an increase or decrease, depending on which interruptions were bigger.

Mathematical theory

The original D/L model started by assuming that the number of runs that can still be scored (called ${\displaystyle Z}$), for a given number of overs remaining (called ${\displaystyle u}$) and wickets lost (called ${\displaystyle w}$), takes the following exponential decay relationship:^[14]

${\displaystyle Z(u,w)=Z_{0}(w)\left({1-e^{-b(w)u}}\right),}$

where the constant ${\displaystyle Z_{0}}$ is the asymptotic average total score in unlimited overs (under one-day rules), and ${\displaystyle b}$ is the exponential decay constant. Both vary with ${\displaystyle w}$ (only). The values of these two parameters for each ${\displaystyle w}$ from 0 to 9 were estimated from scores from 'hundreds of one-day internationals' and 'extensive research and experimentation', though were not disclosed due to 'commercial confidentiality'.^[14]

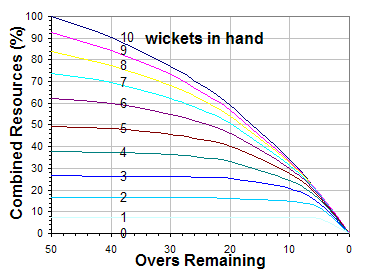
Finding the value of ${\displaystyle Z}$ for a particular combination of ${\displaystyle u}$ and ${\displaystyle w}$ (by putting in ${\displaystyle u}$ and the values of these constants for the particular ${\displaystyle w}$), and dividing this by the score achievable at the start of the innings, i.e. finding

${\displaystyle P(u,w)={\frac {Z(u,w)}{Z(u=50,w=0)}},\,}$

gives the proportion of the combined run scoring resources of the innings remaining when ${\displaystyle u}$ overs are left and ${\displaystyle w}$ wickets are down.^[14] These proportions can be plotted in a graph, as shown right, or shown in a single table, as shown below.

This became the Standard Edition. When it was introduced, it was necessary that D/L could be implemented with a single table of resource percentages, as it could not be guaranteed that computers would be present. Therefore, this single formula was used giving average resources. This method relies on the assumption that average performance is proportional to the mean, irrespective of the actual score. This was good enough in 95 per cent of matches, but in the 5 per cent of matches with very high scores, the simple approach started to break down.^[15] To overcome the problem, an upgraded formula was proposed with an additional parameter whose value depends on the Team 1 innings.^[16] This became the Professional Edition.

Examples

Stoppage in first innings

Increased target

In the 4th India–England ODI in the 2008 series, the first innings was interrupted by rain on two occasions, resulting in the match being reduced to 22 overs each. India (batting first) made 166/4. England's target was set by the D/L method at 198 from 22 overs. As England knew they had only 22 overs the expectation is that they will be able to score more runs from those overs than India had from their (interrupted) innings. England made 178/8 from 22 overs, and so the match was listed as "India won by 19 runs (D/L method)".^[17]

During the fifth ODI between India and South Africa in January 2011, rain halted play twice during the first innings. The match was reduced to 46 overs each and South Africa scored 250/9. The D/L method was applied which adjusted India's target to 268. As the number of overs was reduced during South Africa's innings, this method takes into account what South Africa are likely to have scored if they had known throughout their innings that it would only be 46 overs long, and so the match was listed as "South Africa won by 33 runs (D/L method)".^[18]

Decreased target

On 3 December 2014, Sri Lanka played England and batted first, but play was interrupted when Sri Lanka had scored 6/1 from 2 overs. At the restart, both innings were reduced to 35 overs, and Sri Lanka finished on 242/8. England's target was set by D/L at 236 from 35 overs.^[19] Although Sri Lanka had less resource remaining to them after the interruption than England would have for their whole innings (about 7% less), they had used up 1% more resource before the interruption (2 overs and 1 wicket, about 8%), that the total resource used by Sri Lanka was still slightly more than England would have available, hence the slightly decreased target for England.

Stoppage in second innings

A simple example of the D/L method being applied was the first ODI between India and Pakistan in their 2006 ODI series.^[20] India batted first, and were all out for 328. Pakistan, batting second, were 311/7 when bad light stopped play after the 47th over. Pakistan's target, had the match continued, was 18 runs in 18 balls, with three wickets in hand. Considering the overall scoring rate throughout the match, this is a target most teams would be favoured to achieve. And indeed, application of the D/L method resulted in a retrospective target score of 305 (or par score of 304) at the end of the 47th over, with the result therefore officially listed as "Pakistan won by 7 runs (D/L Method)".

The D/L method was used in the group stage match between Sri Lanka and Zimbabwe at the T20 World Cup in 2010. Sri Lanka scored 173/7 in 20 overs batting first, and in reply Zimbabwe were 4/0 from 1 over when rain interrupted play. At the restart Zimbabwe's target was reduced to 108 from 12 overs, but rain stopped the match when they had scored 29/1 from 5 overs. The retrospective D/L target from 5 overs was a further reduction to 44, or a par score of 43, and hence Sri Lanka won the match by 14 runs.^[21][22]

The DLS method was also used after the rain disruption in the 2023 Indian Premier League final, when Chennai Super Kings had scored 4/0 (0.3 overs) and the Gujarat Titans just scored 214/4 (20 overs). The target was reduced at 171 runs from 15 overs from earlier target of 215 runs from 20 overs for Chennai Super Kings. Chennai Super Kings won by 5 wickets by the DLS method. This was achieved by reaching 171/5 from 15 overs.

An example of a D/L tied match was the ODI between England and India on 11 September 2011. This match was frequently interrupted by rain in the final overs, and a ball-by-ball calculation of the Duckworth–Lewis 'par' score played a key role in tactical decisions during those overs. At one point, India were leading under D/L during one rain delay, and would have won if play had not resumed. At a second rain interval, England, who had scored some quick runs (knowing they needed to get ahead in D/L terms) would correspondingly have won if play had not resumed. Play was finally called off with just 7 balls of the match remaining and England's score equal to the Duckworth–Lewis 'par' score, therefore resulting in a tie.

This example does show how crucial (and difficult) the decisions of the umpires can be, in assessing when rain is heavy enough to justify ceasing play. If the umpires of that match had halted play one ball earlier, England would have been ahead on D/L, and so would have won the match. Equally, if play had stopped one ball later, India could have won the match with a dot ball – indicating how finely-tuned D/L calculations can be in such situations.

Stoppages in both innings

During the 2012/13 KFC Big Bash League, D/L was used in the 2nd semi-final played between the Melbourne Stars and the Perth Scorchers. After rain delayed the start of the match, it interrupted Melbourne's innings when they had scored 159/1 off 15.2 overs, and both innings were reduced by 2 overs to 18, and Melbourne finished on 183/2. After a further rain delay reduced Perth's innings to 17 overs, Perth returned to the field to face 13 overs, with a revised target of 139. Perth won the game by 8 wickets with a boundary off the final ball.^[23][24]

Use and updates

The published table that underpins the D/L method is regularly updated, using source data from more recent matches; this is done on 1 July annually.^[25]

For 50-over matches decided by D/L, each team must face at least 20 overs for the result to be valid, and for Twenty20 games decided by D/L, each side must face at least five overs, unless one or both teams are bowled out and/or the second team reaches its target in fewer overs.

If the conditions prevent a match from reaching this minimum length, it is declared a no result.

1996–2003 – Single version

Until 2003, a single version of D/L was in use. This used a single published reference table of total resource percentages remaining for all possible combinations of overs and wickets,^[26] and some simple mathematical calculations, and was relatively transparent and straightforward to implement.

However, a flaw in how it handled very high first innings scores (350+) became apparent from the 1999 Cricket World Cup match in Bristol between India and Kenya. Tony Lewis noticed that there was an inherent weakness in the formula that would give a noticeable advantage to the side chasing a total in excess of 350. A correction was built into the formula and the software, but was not fully adopted until 2004. One-day matches were achieving significantly higher scores than in previous decades, affecting the historical relationship between resources and runs. The second version uses more sophisticated statistical modelling, but does not use a single table of resource percentages. Instead, the percentages also vary with score, so a computer is required.^[13] Therefore, it loses some of the previous advantages of transparency and simplicity.

In 2002 the resource percentages were revised, following an extensive analysis of limited overs matches, and there was a change to the G50 for ODIs. (G50 is the average score expected from the team batting first in an uninterrupted 50 overs-per-innings match.) G50 was changed to 235 for ODIs. These changes came into effect on 1 September 2002.^[27] As of 2014, these resource percentages are the ones still in use in the Standard Edition, though G50 has subsequently changed.

The tables show how the percentages were in 1999 and 2001, and what they were changed to in 2002. Mostly they were reduced.