Queueing theory is the mathematical study of waiting lines, or queues.^[1] A queueing model is constructed so that queue lengths and waiting time can be predicted.^[1] Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.

Queueing theory has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company.^[1] These ideas were seminal to the field of teletraffic engineering and have since seen applications in telecommunication, traffic engineering, computing,^[2] project management, and particularly industrial engineering, where they are applied in the design of factories, shops, offices, and hospitals.^[3][4]

Spelling

The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is Queueing Systems.

Description

Queueing theory is one of the major areas of study in the discipline of management science. Through management science, businesses are able to solve a variety of problems using different scientific and mathematical approaches. Queueing analysis is the probabilistic analysis of waiting lines, and thus the results, also referred to as the operating characteristics, are probabilistic rather than deterministic.^[5] The probability that n customers are in the queueing system, the average number of customers in the queueing system, the average number of customers in the waiting line, the average time spent by a customer in the total queuing system, the average time spent by a customer in the waiting line, and finally the probability that the server is busy or idle are all of the different operating characteristics that these queueing models compute.^[5] The overall goal of queueing analysis is to compute these characteristics for the current system and then test several alternatives that could lead to improvement. Computing the operating characteristics for the current system and comparing the values to the characteristics of the alternative systems allows managers to see the pros and cons of each potential option. These systems help in the final decision making process by showing ways to increase savings, reduce waiting time, improve efficiency, etc. The main queueing models that can be used are the single-server waiting line system and the multiple-server waiting line system, which are discussed further below. These models can be further differentiated depending on whether service times are constant or undefined, the queue length is finite, the calling population is finite, etc.^[5]

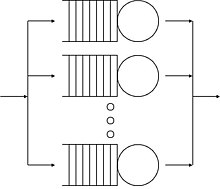
Single queueing nodes

A queue or queueing node can be thought of as nearly a black box. Jobs (also called customers or requests, depending on the field) arrive to the queue, possibly wait some time, take some time being processed, and then depart from the queue.

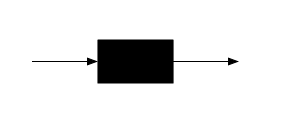
However, the queueing node is not quite a pure black box since some information is needed about the inside of the queueing node. The queue has one or more servers which can each be paired with an arriving job. When the job is completed and departs, that server will again be free to be paired with another arriving job.

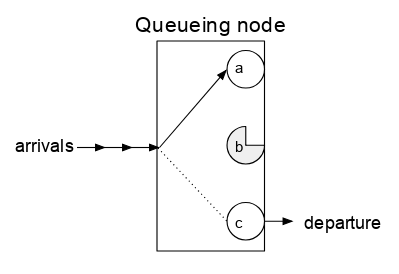
An analogy often used is that of the cashier at a supermarket. (There are other models, but this one is commonly encountered in the literature.) Customers arrive, are processed by the cashier, and depart. Each cashier processes one customer at a time, and hence this is a queueing node with only one server. A setting where a customer will leave immediately if the cashier is busy when the customer arrives, is referred to as a queue with no buffer (or no waiting area). A setting with a waiting zone for up to n customers is called a queue with a buffer of size n.

Birth-death process

The behaviour of a single queue (also called a queueing node) can be described by a birth–death process, which describes the arrivals and departures from the queue, along with the number of jobs currently in the system. If k denotes the number of jobs in the system (either being serviced or waiting if the queue has a buffer of waiting jobs), then an arrival increases k by 1 and a departure decreases k by 1.

The system transitions between values of k by "births" and "deaths", which occur at the arrival rates ${\displaystyle \lambda _{i}}$ and the departure rates ${\displaystyle \mu _{i}}$ for each job ${\displaystyle i}$. For a queue, these rates are generally considered not to vary with the number of jobs in the queue, so a single average rate of arrivals/departures per unit time is assumed. Under this assumption, this process has an arrival rate of ${\displaystyle \lambda ={\text{avg}}(\lambda _{1},\lambda _{2},\dots ,\lambda _{k})}$ and a departure rate of ${\displaystyle \mu ={\text{avg}}(\mu _{1},\mu _{2},\dots ,\mu _{k})}$.

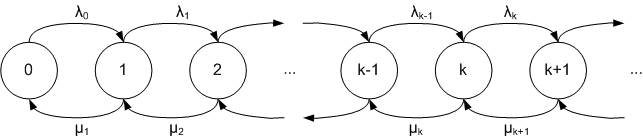
Balance equations

The steady state equations for the birth-and-death process, known as the balance equations, are as follows. Here ${\displaystyle P_{n}}$ denotes the steady state probability to be in state n.

${\displaystyle \mu _{1}P_{1}=\lambda _{0}P_{0}}$

${\displaystyle \lambda _{0}P_{0}+\mu _{2}P_{2}=(\lambda _{1}+\mu _{1})P_{1}}$

${\displaystyle \lambda _{n-1}P_{n-1}+\mu _{n+1}P_{n+1}=(\lambda _{n}+\mu _{n})P_{n}}$

The first two equations imply

${\displaystyle P_{1}={\frac {\lambda _{0}}{\mu _{1}}}P_{0}}$

and

${\displaystyle P_{2}={\frac {\lambda _{1}}{\mu _{2}}}P_{1}+{\frac {1}{\mu _{2}}}(\mu _{1}P_{1}-\lambda _{0}P_{0})={\frac {\lambda _{1}}{\mu _{2}}}P_{1}={\frac {\lambda _{1}\lambda _{0}}{\mu _{2}\mu _{1}}}P_{0}}$.

By mathematical induction,

${\displaystyle P_n=\frac{{\mathrm{\lambda <!--\; \lambda \; -->}}_{n-<!--\; -\; -->1}{\mathrm{\lambda <!--\; \lambda \; -->}}_{n-<!--\; -\; -->2}\cdots <!--\; \cdots \; -->{\mathrm{\lambda <!--\; \lambda \; -->}}_0}{{\mathrm{\mu <!--\; \mu \; -->}}_n{\mathrm{\mu <!--\; \mu \; -->}}_{n-<!--\; -\; -->1}\cdots <!--\; \cdots \; -->{\mathrm{\mu <!--\; \mu \; -->}}_1}{P}_0=P_0\underset{i=0}{\overset{n-<!--\; -\; -->1}{\prod <!--\; \prod \; -->}}\frac{{\mathrm{\lambda <!--\; \lambda \; -->}}_i}{{\mathrm{\mu <!--\; \mu \; -->}}_{i+1}}}$Zdroj:https://en.wikipedia.org?pojem=First-come,_first-served
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---