Mocninná funkcia

Mocninová funkcia je typ elementárnej matematickej funkcie jednej premennej, v ktorej vystupuje len jeden člen s mocninou. Mocninová funkcia je špeciálnym prípadom polynomickej funkcie. Najznámejším príkladom mocninovej funkcie je špeciálny prípad kvadratickej funkcie. Podľa stupňa mocniny premennej sa rozlišujú mocninové funkcie rôznych druhov. V začiatkoch budovania matematickej teórie o funkciách boli predmetom skúmania práve mocninové funkcie, z ktorých bolo odvodené množstvo vlastností a vzťahov. K mocninovým funkciám sa neskôr pridružili aj ďalšie funkcie a spolu vytvorili skupinu pod názvom elementárne funkcie. Pomocou základných mocninových funkcií je možné modelovať veľmi veľa jednoduchých situácii a javov. Svoje opodstatnenie našli v samotnej matematike, vo fyzike, ekonómii a v mnohých ďalších oblastiach.

Krajne asymetrickým rozdelením/rozložením sa zaoberal napr. český geograf, demograf a štatistik Jaromír Korčák v dielach Deux types fondamentaux de distribution statistique (1938) alebo Přírodní dualita statistického rozložení (1941).

Definícia

Nech $a\in \mathbb {R} ,n\in \mathbb {R} -\{0\}$ . Potom predpis

$f:\mathbb {R} \mapsto \mathbb {R} ;x\mapsto f(x)=n\cdot x^{a}$

nazývame mocninová funkcia s reálnym mocniteľom. Ak $a\in \mathbb {Z} ^{-}$ potom ide o mocninovú funkciu so záporným celočíselným mocniteľom. Ak $a\in \mathbb {Z} ^{+}$ ide o mocninovú funkciu s kladným celočíselným mocniteľom alebo s prirodzeným mocniteľom.

Druhy mocninových funkcií

Mocninové funkcie sa rozlišujú podľa stupňa mocniny premennej, ktorú obsahujú. Lineárna a konštantná funkcia sú špeciálnym prípadom mocninovej funkcie. Obvykle sa ale v definícii týchto funkcii nepíšu mocniny. V nasledovnej tabuľke sú mocninové funkcie s ich názvami nanajvýš tretieho stupňa:

Stupeň	Predpis funkcie	Názov
$a={-1}$	$f(x)={\frac {n}{x}}$	nepriama úmernosť
$a=0$	$f(x)=n$	konštantná funkcia
$a=1$	$f(x)=nx$	lineárna funkcia
$a=2$	$f(x)={nx^{2}}$	kvadratická funkcia
${a=3}$	$f(x)=nx^{3}$	kubická funkcia

Vlastnosti mocninových funkcií

Vlastnosti mocninových funkcií sú závislé od stupňa mocniny. Grafy tohto typu funkcií sú rôzne, čo závisí opäť od veľkosti a druhu mocniteľa. Napríklad parabola alebo hyperbola.^[1] Mocninové funkcie s kladným mocniteľom majú tú spoločnú vlastnosť, že všetky prechádzajú začiatkom sústavy súradníc. Ostatné vlastnosti sa navzájom líšia. Keďže vlastnosti závisia od mocniteľa, je lepšie obmedziť sa na funkcie s celočíselným párnym resp. nepárnym mocniteľom.

Funkcia s kladným párnym mocniteľom

${n\in \mathbb {R} -\{0\}},a\in \mathbb {Z} ^{+}$
$f:\mathbb {R} \mapsto \mathbb {R} ;x\mapsto f(x)=n\cdot x^{2a}$

Vlastnosť	Rozbor	Graf
definičný obor a obor hodnôt	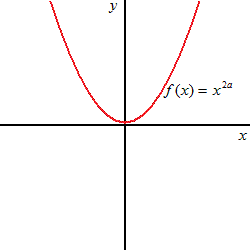${D(f)}=\mathbb {R}$ ${H(f)}=\mathbb {R} _{0}^{+}$
prostá funkcia	Funkcia nie je prostá, pretože neplatí nasledovná implikácia pre ľubovoľnú dvojicu čísel ${}$ : $x_{1}\neq x_{2}\Rightarrow n\cdot x_{1}^{2a}\neq n\cdot x_{2}^{2a}$
monotónnosť	Ak $n$ je kladné, potom funkcia je klesajúca na intervale $(-\infty ;0)$ a rastúca na intervale $(0;+\infty )$ , v opačnom prípade je funkcia rastúca na intervale $(-\infty ;0)$ a klesajúca na intervale $(0;+\infty )$

[1]